*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
대부분의 데이터는 추세 뿐만 아니라 계절성 또한 띈다.
아래 그래프를 살펴보면, 평균이 변하는 Trend도 보이지만, 일별이다보니, 요일에 따라 위 아래로 그래프가 진동하면서 이동하는 패턴을 확인할 수 있다. (평일에는 비슷한 수준이나 주말마다 오르는 형태.)

ARIMA에서 차분을 통해 추세를 제거할 수 있었으나, 문제는 차분만으로는 계절성이 완전히 제거되지 않을 수 있다는 점이다. 직관적으로 생각해봐도, 만약 12개월 주기가 있다면, $X_t$와 $X_{t+12}$ 사이에 관계가 있을 텐데, 차분의 경우 한 시점간의 차이만을 고려하므로, 이를 따로 다루어 주어야 함을 생각해 볼 수 있다.
계절성 차분 (Seasonal Differencing)
이렇게 계절성이 존재하는 데이터를 다룰 때 사용하는 것이 계절성 차분이다. 아래 그래프를 보면, 그냥 차분을 진행하면서 시계열의 평균은 일정해졌지만, 같은 빈도로 특정한 패턴이 여전히 남아있다. 아래 그림은 여기에 계절성 차분을 추가함으로써 일정한 데이터가 됨을 확인할 수 있다.
계절성 차분은 인근 두 계절 값의 차이를 산출하는 것으로, 주기에 따라 주기만큼 차이나는 이전 시점의 데이터를 빼주는 작업이라고 보면된다.

계절성(Seasonal) ARIMA 모형: SARIMA;
이번엔 ARIMA를 계절성 존재 시에도 사용할 수 있도록 하는 SARIMA에 대해 알아보자. 먼저 SARIMA가 어떤 방식으로 유도된 모델인지 논리의 전개를 한번 확인해보자.

위 그림의 내용을 하나하나 따라가보자.
주기가 12인 데이터가 존재할 때, 각 월만 모아놓은 데이터 셋 (EX: 1월의 경우 2001-01, 2002-01 ... 2022-01)에 대해 이 데이터셋들이 정상성을 가지고, MA(1) 모형을 따른다고 가정하면 아래 식처럼 나타낼 수 있다. 여기서 $\alpha$는 오차항으로, 12월 단위로 보았을 때 오차항 간에는 상관관계가 없다.
$$Z_t = (1-\Theta B^{12})a_t$$
첫번째식
그렇다면 한 시점 차이의 오차 $\alpha_t$와 $\alpha_{t-1}$은 상관관계가 없을까? 인근 월은 계절성이 존재한다면 오차항 간의 상관관계가 있다고 보는 것이 합리적이다. *
*가장 우리에게 익숙한 $sin$함수를 예시로 설명해보겠다.
$Z_t = sin(\frac{\pi}{2}t) + a_t$ 라는 실제 데이터가 있다고 가정하고($a_t$ = white noise), 우리가 추정한 모형은 $(1-\Theta B^4)\alpha_t$라고 해보자. 편의상 $(1-\Theta B^4) = K$로 두겠다.
주기 $t = 4 (=2\pi)$ 간격으로 뽑은 실제값 $Z_t = 0 + a_t (t=4, 8, ...)$ 에 대해서 추정된 함수값은 $K\alpha_t$ 이므로, $K\alpha_t = a_t$로 표현되고, 당연히 $a_t$간의 상관관계가 없으니 $\alpha_t$ 역시 상관관계가 없다.
주기 $t=1 (=\frac{\pi}{2})$ 간격에서는 실제값 $Z_t = 1 + a_t , Z_t = a_t, Z_t = -1 + a_t, Z_t = 0 + a_t$
*여기서 각 $t = (4n+1, 4n+2, 4n+3, 4n+4, n$은 정수) 으로 진동하는 반면 추정된 함수값은 t에 상관없이 같은 값$K\alpha_t$으로, $K \alpha_t = sin(\frac{\pi}{2}t) + a_t$가 된다.
시점 $4n + 1$과 $4n + 2$를 비교하면, $K \alpha_1 = 1 + a_1, K \alpha_2 = 0 + a_2$로, $\alpha_1$과 $\alpha_2$와의 상관관계가 음(-)이고,
시점 $4n + 3$과 $4n + 4$를 비교하면, $K \alpha_3 = -1 + a_3, K \alpha_4 = 0 + a_4$로, $\alpha_3$과 $\alpha_4$와의 상관관계가 양(+)이다.
즉 t값이 변하면서 $\alpha$간에 양과 음의 상관관계가 번갈아가면서 생기므로, $\alpha$ 사이에는 상관관계가 존재한다.
이는 다르게 생각하면, 추정된 함수 $(1 - \Theta B^4)\alpha$만으로 실제값 $Z_t$를 충분히 표현하지 못한다는 것이다.
따라서 오차항의 상관관계를 표현하기 위해서 아래와 같이 $\alpha_t$를 또다른 오차항의 모델로 나타내는 것이 필요하다. 오차항 $\alpha$가 MA(1)을 따른다고 하면 아래와 같은 식이 된다.
$$ \alpha_t = (1-\theta B)\alpha_t$$
첫번째 식($Z_t$에 대한 식)의 $\alpha_t$대신에 아래 식을 대입하게 되면 최종적으로 아래 식과 같은 형태가 된다. 이를 비계절성 MA와 계절성 MA를 가지고 있는 $ARMA(0,1) \times (0,1)_{12}$ 라고 표기한다. (여기서 12는 s 즉 주기를 의미함.)
$$Z_t = (1-\Theta B)(1-\Theta B^{12})a_t$$
이를 다시 ARIMA로 표현하면 $ARIMA(0,0,1) \times (0,0,1)_{12}$가 된다. 정확한 표기는 위의 유도예시 그림을 참조하자.
아래 예시를 살펴보면 계절성 ARIMA를 일반적으로 어떻게 표기하는지, 이를 어떻게 해석하는지 이해하는데에 도움이 된다. 여기서 대문자 D가 아까 설명한 계절성 차분이다.

SARIMA 모형을 구축하는 과정과 실제 예시를 통해 살펴보면, 내용이 정리가 될 것이다.
모형의 식별 및 추정 과정

단계 2)에서 계절성 차분을 먼저 실시하는 것은 추천사항이며 무엇이 먼저인지는 크게 중요하지 않으나, 계절성이 강한 데이터의 경우 계절성 차분만으로 stationary가 성립되는 경우가 있어 이런 순서로 진행한다고 한다. (반면 이러한 경우에도 비계절성 차분을 먼저 하면 계절성 차분을 해야 stationary가 된다.) 자세한 내용은 아래 글을 참조하자.
https://otexts.com/fppkr/stationarity.html
8.1 정상성과 차분 | Forecasting: Principles and Practice
2nd edition
otexts.com
단계 3) 에서는 ACF, PACF를 바탕으로 $p, q, P, Q$를 결정하는데, ARMA 모델에서도, AR, MA, ARMA 모형의 이론적 ACF와 PACF의 특징을 바탕으로 실제 데이터에 적합한 $p$와 $q$를 결정했듯, 여기서도 마찬가지이다.
- ACF 산출 방법 예시
이론적 ACF 산출 자체는 $Z_t$ 대신 $W_t$를 이용해 계산하는 것 외의 차이는 없지만, 그래프 추이와 해석은 달라진다.
기존 MA(1) 모형의 경우 ACF가 $q$ 시점 이후 절단패턴을 보였다면, 차분시계열($W_t$)는 시차가 11, 12, 13 이런 경우에도 값을 갖게 되어 해석이 어렵다. 따라서 다양한 모형의 패턴들을 보고 이를 참조해 결정하는 것이 일반적인 방법론이라고 한다. (해석은 아래에서 설명할 예정)

실제 사례를 통해 단계 1~5를 따라가 보자.
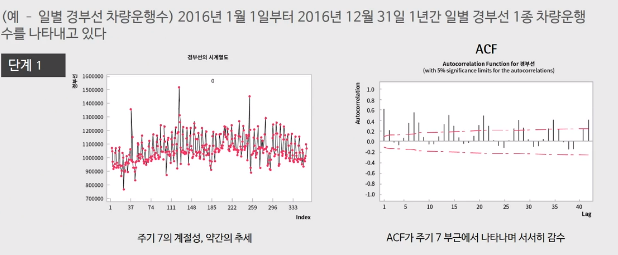
단계1) 아까 위에서 본 경부선 차량운행수 데이터를 보면 ACF에서 7을 주기로 큰 값이 나타나는 것을 볼 수 있다. 이는 계절성이 있음을 의미하며, 비정상성을 띈다고 볼 수 있다.
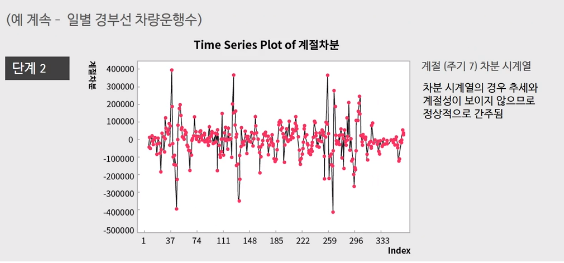
단계2) 주기가 7임을 확인했으니, 계절차분을 먼저 $s=7$로 씌우게 되면 $(Z_t - Z_{t-7}) = (1-B^7)Z_t$ 추세는 없어지고 정상적인 모습을 띈다. 아래 왼쪽 그래프를 보면 추가적인 비계절성 차분은 필요없어 보인다. -> $d = 0, D = 1$
차분 시계열에 대해 ACF, PACF를 확인해보면 ACF에서는 첫번째 시점부터 지수적으로 감소, PACF는 첫번째 시점에서 0 cutoff 되므로, AR(1) 모형으로 볼 수 있다. ->$p = 1, q = 0$
다음으로 ACF, PACF를 주기 = 7로 살펴보면(아래 ACF, PACF 그래프의 7n번째 데이터만 확인해보자) ACF는 첫번째 주기에서 cutoff, PACF는 지수적으로 감소함을 확인할 수 있다. -> MA(1) 모형으로 $P = 0, Q = 1$
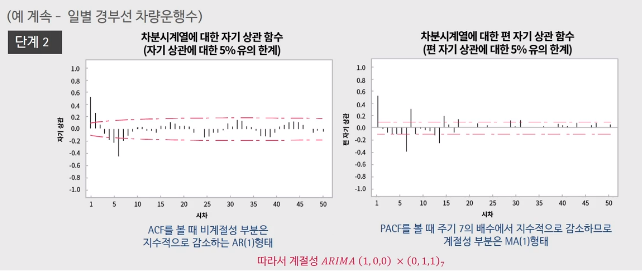
이 두개를 결합하면 $ARIMA(1,0,0) \times (0,1,1)_7$ 즉 비계절성은 차분을 안한게 AR(1), 계절성은 차분을 한게 MA(1)이라고 볼 수 있다.
단계4)에서는 모델 파라미터 추정을 진행해야한다. 아래는 EVIEWS, MINITAB을 활용한 추정 결과이다.
AR1은 $\psi$를, S(easonal)MA1은 $\theta$를 추정해야하는데, p-value를 보면 유의함을 확인할 수 있다.
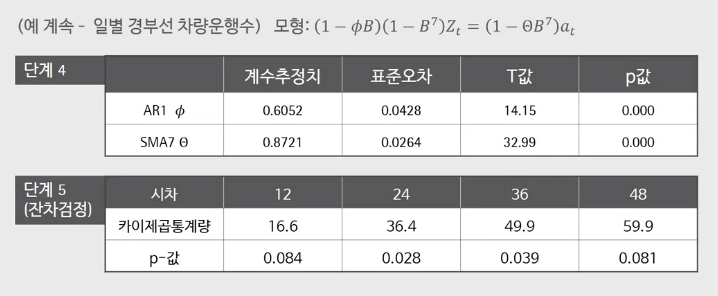
단계5) 마지막으로, 잔차가 랜덤성(White Noise를 띄는지)을 가짐을 확인해야하는데, 위 그림에서 보이듯 24, 36 시차에서 p-value가 낮게 나와, 잔차의 평균이 0이 아님. 즉 아직 완벽한 White Noise만 남았다 라고는 볼 수 없다.
다만, 큰 시차의 차이인 48에서 H0 : E[residual] = 0이 기각되어, 이 경우 잔차 검정 테스트에 통과(Residual이 White Noise다.)되었다고 볼 수 있는데, 실제 상황에서는 이런 경우 큰 시차에서 랜덤성을 보였으므로 이 모형이 제대로 식별된 모형으로 본다고 한다.
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-2 GARCH: ARCH의 일반화 형태 (0) | 2023.03.28 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-1 오차의 조건부 분산 개념 및 ARCH 모형 (0) | 2023.03.28 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week4-1 비정상적 시계열 모형화를 위한 ARIMA 모형 (0) | 2023.03.22 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-3 최소평균오차 기반의 ARMA 모형 예측치 유도 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-2 ARMA모형의 파라미터 추정을 위한 최우추정법 (0) | 2023.03.15 |



