https://peerj.com/preprints/3190.pdf
2017년 9월에 발표한 Article로서, "at Scale"은 '대규모로', 혹은 '전체의' 등으로 해석된다. 논문 내용을 살펴보면 Prophet이 지향하는 바는 다양한 시계열 예측 프로세스의 모든 과정을 시계열 데이터 분석을 할 줄 모르는 사람도 할 수 있도록 시계열 분석의 A-to-Z를 진행할 수 있게끔 만든 패키지라고 보면 된다.
Introduction
대부분의 기업에서는 capacity planning (다음 달 생산을 위해 사람이 얼마나 필요한지, 원자재가 얼마나 필요한지) 등 다양한 이유로 Forecasting 즉 예측을 진행한다. 하지만 완전히 자동화된 예측 모듈은 튜닝하기가 어렵고 대부분 유동적이지 못해 새로운 가정(assumptions, 다음달에 새로운 제품이 출시된다)이나 휴리스틱(heuristic: 경험적으로 매달 말에 예측보다 더 많은 주문이 들어온다.)을 적용하기가 까다롭다.
또한 기업에서 이러한 데이터분석을 진행하는 분석가들의 경우 도메인 지식으로는 전문가 수준이나, 시계열 예측 모형을 만드는 데에는 그리 전문적이지 못한 경우가 많다. 이런 경우 도메인 전문가로서의 지식을 시계열 예측에 적용하는 것이 예측을 더 우수하게 만들 수 있으나, 두 가지가 동시에 충족되지 못하는 경우가 많다.
페이스북에서는 이러한 문제들을 해결할 수 있도록, analyst-in-the-loop 시스템을 가진, 즉 인간의 개입과 자동화 시스템이 어우러진 모델을 개발하고자 하였다.

이를 충족시키기 위해 생각해 보아야 할 문제는 다음과 같다.
- Configurable : 새로운 정보나, 인간이 새로운 이벤트 등을 모델에 집어넣고 싶을 때 쉽게 조정이 가능한 모델이어야 한다는 것. 즉, 내가 예측하고 싶은 정보가 월 단위 시계열성이 있거나, 아니면 이번 주에 새로운 제품을 출시한다던가 할 때, 파라미터 조정이나 이벤트 지정 등으로 모델이 더 정확한 예측을 할 수 있게 만들 수 있어야 한다.
- Fast : 모델을 학습시키는데 만약 1시간 넘게 시간이 걸리면, 다양한 모델을 돌려보고 조정하기에 너무 Load가 많이 들어간다. 따라서 모델 학습시간이 최대한 빨라야 한다.
- At Scale: 만약 일반적이고 Smooth한 시계열 데이터에만 적용이 가능하다면, 모두가 이를 안심하고 사용하기는 어렵다. 예를 들어 크리스마스 트리의 수요를 예측하고자 한다면 주로 크리스마스 이전 일주일 정도에만 매출이 증가할 확률이 높을 것이다. <- 이런 경우라도 예측 결과가 타당해야 한다. 즉 데이터의 종류나 특징에 상관없이 "우수한" 예측이 동적으로 가능해야 한다.
- Interpretable Metrics: 다양한 시계열 문제들에 적용할 수 있는 적합한 평가지표가 존재해야한다. 또 이를 바탕으로 Alarm (poor performance나 potential problems가 존재하는 경우, 분석가에게 이를 알려야함)이나 Visualization (그래프)등을 제공해야 하므로, 적절한 Threshold나 분석가가 쉽게 파악할 수 있는 Visualizaiton 방식이 필요하다.
Features of Business Time Series
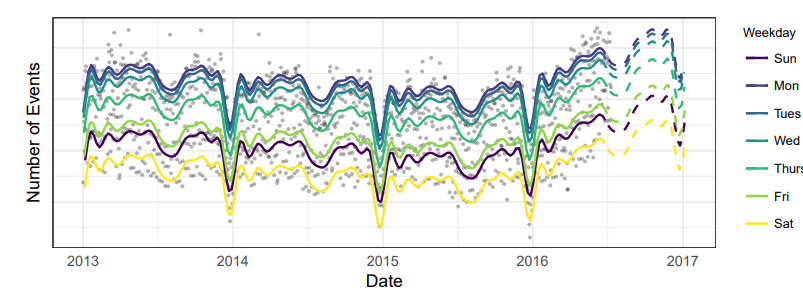
페이스북에서는 이벤트 플렛폼 기능이 있는데, 이를 통해 사람들을 초대하거나 할 수 있다. 아래 그림은, 페이스북에서 이벤트가 열린 횟수를 기록한 데이터이다. X축의 경우 n번 째 주를 의미하고, y축은 각 주의 특정 요일에 이벤트가 발생한 횟수를 매핑한 것이다.

데이터를 살펴보면 먼저 2014년 전후로 이상치들이 존재하고(Outliers), 세로축으로 선을 그으면 주 단위 계절성(Weekly Cycle)을, 연단위로 나누어 가로 기준 변화를 보면 연단위 시계열성(Yearly Cycle)을 확인할 수 있고, 크리스마스나 1월 1일의 경우 이벤트 개수가 매우 감소하는 것(end of year dip)을 확인할 수 있다. 또한 마지막 6주가량에서 trend가 증가하는 것을 확인할 수 있다.
논문에서는 이러한 형태의 데이터가 대부분의 시장에서 확인할 수 있는 시계열 데이터의 형태이며, 이상치, 사이클, 트랜드 변화 등 다양한 내용을 모두 담고 있는 데이터 (At Scale을 보여주기에 가장 적합)이므로 이 데이터를 기준으로 앞으로의 내용을 전개해 나간다.
다음 그림은 위의 데이터에 대해 각각 auto.arima, ets, snaive, tbats 시계열 예측 모델을 적용시킨 결과물이다.
먼저 ARIMA를 살펴보면 연말에 생기는 end of year dip 현상에 제대로 대응하지 못하고 예측에 실패하는 것을 볼 수 있고, weakly Seasonality가 전혀 반영되지 않아, 각 요일별 모든 예측이 하나의 line으로 수렴하는 현상을 보여준다.
마찬가지로 나머지 모듈들의 경우에도, end of year에 과한 반응이 일어나는 것을 볼 수 있다.

이러한 문제점을 해결함과 동시에, 직관적 configuration이 가능한 모델을 만들기 위해 어떤 작업을 거쳤는지 다음 장에서 확인해보자.
The Prophet Forecasting Model
Prophet의 가장 기본적 basis는 decomposable time series model 즉, Time series 데이터셋이 가지고 있는 특성들 (Trend, Seasonality 등)을 모두 분리하여 예측하는 모델이다.
$$ y(t) = g(t) + s(t) + h(t) + \epsilon_t$$
g(t)는 trend function으로서 non-periodic 즉 주기적이지 않은 변화를 예측하는 함수
s(t)는 반대로 periodic한 변화를 감지하는 함수
h(t)는 holiday에 대한 효과를 반영하기 위한 함수로, 하루일 수도 있고, holiday가 발생하는 주간을 다룰 수도 있다.
$\epsilon_t$는 error term으로, 위의 세가지 함수로 설명되지 않는 특이한 변화들을 다루기 위한 수식이다. 일반적인 시계열 모델들과 같이 정규분포를 따른다는 가정을 둔다.
여기서 Seasonality term을 adding 하는 방식으로 표기했지만, multiplicative seasonality의 경우(진폭이 증가하는 계절성) log transform을 g(t)에 적용하는 방식으로 적용할 수 있다고 한다.
논문에서는 이러한 Decomposable model을 Generalized Additive Model(GAM)과 유사하다고 설명하는데, regressor (input x)로서 time만을 사용하지만, 내부에 작용하는 각각의 함수들은 time을 input값으로 사용하는 linear or nonlinear smoother 이기 때문이다. *
*간단하게 말하자면 GAM은 일반적인 regression model $y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 +... $의 꼴에서 beta 대신에 linear함수 혹은 nonlinear함수 f1 ~ fn 으로 구성된 $y = \beta_0 + f_1(x_1) + f_2(x_2) ... $을 사용한다. 이와 같이 prophet 모델도, linear 혹은 nonlinear 함수 g(t), s(t), h(t)의 합으로 구성되어 있으므로 유사한 형식이라는 것.
이렇게 GAM 형식을 사용하는 것의 장점은, 일단 시계열 분해(decompose)가 쉽고 새로운 컴포넌트가 추가되어도 이를 다루는데 무리가 없다는 점이다. 예를 들어 새로운 Seasonality가 관측되었을 때 그냥 새로운 함수 s_1(t)를 만들어서 fit하면 되니 조정이 쉽다.
또 GAM 형식을 사용하면 backfitting 이나 L-BFGS (둘 모두 최적화 알고리즘의 일환으로 additive 통계모델에 적절함)을 이용할 수 있어 빠른 속도로 학습이 가능하다.
Prophet은 기존의 ARIMA와 같은 방식과 다르게 forecasting problem을 curve-fitting excercise문제로 바꿔버림으로서 기존의 time series모델과는 아예 내부적으로 다른 방식을 사용했다. 다른 Time series 모델의 경우, 시간적으로 가지고 있는 데이터의 Dependency를 고려했다면 여기서는 그러한 방식의 장점을 포기하고, 아래와 같은 다른 장점들을 얻을 수 있었다.
- Flexibility(유동성): 쉽게 다양한 주기의 Seasonality를 추가할 수 있고, 분석가가 다른 trend의 가정들을 만들 수 있게 했다. (결국 계절성과 추세 조정을 유동적으로 할 수 있게 했다는 의미)
- 편의성: Arima 모델과는 다르게, regularly spaced 될 필요가 없다. 즉 중간중간 데이터가 빠져있어도(이상치 제거 등으로) 보간법을 사용해서 메꿀 필요가 없고, 같은 기간으로 데이터를 입력할 필요가 없음.
- Fast: Fitting 시간이 굉장히 빠르기 때문에 분석가가 다양한 모델을 시도해 볼 수 있음.
- Interpretable: 예측 모델이 굉장히 해석하기 쉬운 파라미터로 구성되어 있기 때문에 데이터에 대한 새로운 가정이 추가되어도 이를 적용하기 쉽다. 또한 regression 에 익숙한 분석가들이 새로운 component를 추가하는 것 또한 가능하다.
결국 이러한 formulation이 앞서 Introduction파트에서 "생각해 보아야 할 점"에서 얘기한 Configurable, and Fast 조건을 만족시키기에 적합한 모델이라는 것이다.
이후로는 각각의 component(Trend, Seasonality, holidays functions)들이 어떻게 구축되었는지 상세하게 알아보자.
The Trend Model
페이스북에서는 Trend를 추정하기 위한 모델로 saturating growth model, piecewise linear model 두 가지 모델을 제시했다.
Nonlinear, Saturating Growth
성장 예측 문제에서 가장 중요한 것은 집단이 지금까지 어떻게 성장해 왔는지와, 계속 성장한다면 어떻게 진행 할것인지를 보는 것이다. 논문에서는 페이스북 이용자 수의 성장그래프가, 자연생태계에서의 개체군(population)증가와 유사하다고 한다.

https://www.nature.com/scitable/knowledge/library/an-introduction-to-population-growth-84225544/
An Introduction to Population Growth | Learn Science at Scitable
Dary, D. A. The Buffalo Book: The Full Saga of the American Animal. Chicago, IL: Swallow Press, 1989. Elton, C. Periodic fluctuations in the numbers of animals: Their causes and effects. British Journal of Experimental Biology 2, 119-163 (1924). Gates, C.
www.nature.com
이러한 비선형 성장은 carrying capacity* 를 saturate* 하는 형태이다.
*Carrying capacity는 환경 생태학 개념에서 쓰이는 용어로, 간단히 정의하자면 자연적 평형상태 즉 자연상태에서 도달할 수 있는 최대의 양을 의미한다. 논문에서 든 예시로는 Facebook의 이용자 수는 인터넷 이용자 수를 넘을 수 없으므로, Facebook population growth 의 carrying capacity로 인터넷 이용자 수로 정의한다.
*Saturate는 '포화'로, 수학적인 정의로는 그래프의 양끝으로 도달할 수록 기울기가 0으로 수렴하는 형태를 의미한다. Saturating function의 예시로는 로지스틱(sigmoid)함수가 있다.
이를 통해 논문에서는 비선형 Trend를 추정하는 함수로, 이러한 C를 saturating 하는 로지스틱 함수를 정의했다.
$$ g(t) = \frac{C}{1+e^{(-k(t-m))}}$$
C: Carrying capacity, k: Growth Rate, m: offset parameter.


그래프를 통해 이 함수가 어떤 형태인지 알아보자. 먼저 Carrying Capacity 인 C는 그래프의 max지점을 정의한다. Growth rate k는 그래프의 기울기를 결정하며, m은 그래프의 중심을 결정한다. 위 그림에서 볼 수 있듯, m = 2일 때 그래프의 중심은 t = 2에서 발생하고, m = 0일때는 t = 0 에서 발생한다.
논문에서는 위 수식과 정확히 맞지 않는 두 가지 중요한 growth의 특징을 알아냈는데, 첫 번째로, carrying capacity가 상수가 아니라는 것이다. 이에 carrying capacity C를 시간에 따라 변하는 함수 C(t)로 바꾸었다. 두 번째로, growth rate가 상수가 아니라는 점이다. 특히 새로운 제품이 출시된 경우 growth rate가 확실하게 변하는 경향이 있어 모델에서도 이를 반영할 수 있는 방법이 필요했다.
이에 모델에서 growth rate가 바뀔 수 있는 지점을 changepoints라고 정의하고 j번째 changepoint가 발생하는 time index를 $s_j$ = 1,2,3,... S이라고 두었다. 또한 rate에 조정을 가하는 파라미터 $\vec{\delta} \in \mathbb{R}$ 와 델타의 각 component $\delta_j$를 정의하였다.
이를 이용해 기존의 simple 한 k였던 growth rate를 $k + \sum_{j:t>s_j} \delta_j $ 로 바꿨다. 보기에는 어려운 수식이나 간단히 생각해보면 현재 time index가 t일때, t시점 이전에 발생한 changepoints(event) $s_j$가 존재하면, 이에 해당하는 $\delta_j$들을 모두 더해준다는 의미이다.
예를 들면 t = 4시점에 growth rate를 계산하고자 한다. 기본 growth rate k = 1이고, t=1 시점에 제품출시 $s_1$이 발생했고, 이 때 변화율에 생기는 차이가 $\delta_1 = 3$이라고 하자. 다음 제품 출시$s_2$는 t = 5시점에 발생한다. 그럼 현재의 변화율은? 1+3 = 4.
1(기본 변화율 k) + 3(t=4시점 이전에 발생한 changepoint는 $s_1$하나이므로 $\delta_1$만 더해준다.) = 4
논문에서는 아래의 component를 가지는 a vector $\vec{a(t)} \in \{0, 1\}^S$ 를 정의해

식을 간단하게 정의한다. $ k + \vec{a(t)}^T\vec{\delta}$
이렇게 growth rate를 계단식으로 결정하면 기존의 연속함수였던 로지스틱 함수가 끊기게 되는 문제가 생긴다. 이를 보정하기 위해 event 발생 시점의 함수값을 일치시키기 위해 $\gamma_j$를

위와 같이 정의하고, 로지스틱 growth 모델을 아래와 같은 형식으로 바꿔준다.
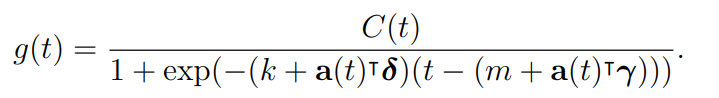
매우 복잡해보이나, 단순계산으로 구할 수 있는 것이라고 하니 (실제 논문에서는 easily calculated 라는 명칭으로 이를 표현한다.), 시간 여유가 된다면 한번 구해보는 것도 좋을 듯 하다.
여기서 C(t)의 경우, 도메인 지식을 가지고 있는 전문가가 직접 지정해줘야 하는 파라미터로, 실제 패키지를 이용할 때 이를 결정하는 것이 가장 중요한 Task가 된다고 한다.
Linear Trend with Changepoints
만약 growth 이 saturating function의 형태를 따라가지 않는 형태의 예측 문제에서는 $e^{-z}$ term안에 들어있는 z부분만 가져와서 아래와 같은 모델로 사용하면 된다.

Nonlinear trend 함수와 Linear trend 함수 모두 수식만으로는 명확히 이해가 되지 않을 것 같아, 실제 prophet에서 trend를 분석한 결과를 가져와 보았다.

논문에서 실제로 trend 함수에 대해 "piecewise"라는 표현을 사용하는데, 그래프를 보면 알 수 있듯 중간 중간 Linear 함수와 nonlinear 함수가 연속된 형태임을 알 수 있다. 특히 2019년 3월에 비선형인게 확실히 보이고 그 이후에 선형 그래프의 형태를 띈다. 즉 Trend가 선형 형태를 띄는 구간은 선형함수로 추정하고, 비선형 형태를 띄는 구간에는 비선형 함수로 추정한다는 것.
만약 선형 함수만 사용한다면 이런 형태일 것이다. (이벤트 발생 시점마다 그래프의 기울기가 변하는 형태)

Automatic Changepoint Selection
이렇게 이벤트가 발생하는 changepoint $s_j$는 도메인에 대해 잘 아는 분석가가 직접 입력하거나(다음 달에 우리 회사 제품 출시), 혹은 여러 후보자 세트에서 자동적으로 골라지는 방법이 가능하다. 자동 선택은 선형과 비선형 함수 내에 존재하는 $\delta$벡터에 임의값을 Sparce(듬성듬성하게)하게 집어넣으면 학습을 통해 자동적으로 얻어낼 수 있다.
논문에서는 initializing 방법으로, 라플라스 분포를 이용해 $\delta_j$를 Sparse하게 Generate하는 방식을 사용한다. $\delta_j \sim Laplace(0,\tau)$ 여기서 파라미터 tau값은 growth rate를 얼마나 유동적으로 변경할지를 결정하는 지표가 된다. 아래 그림은 라플라스 분포의 확률밀도함수를 가져온 것으로, tau값이 증가할 수록 generate되는 $\delta$의 절댓값이 증가할 확률이 오르는 것을 직관적으로 알 수 있다.
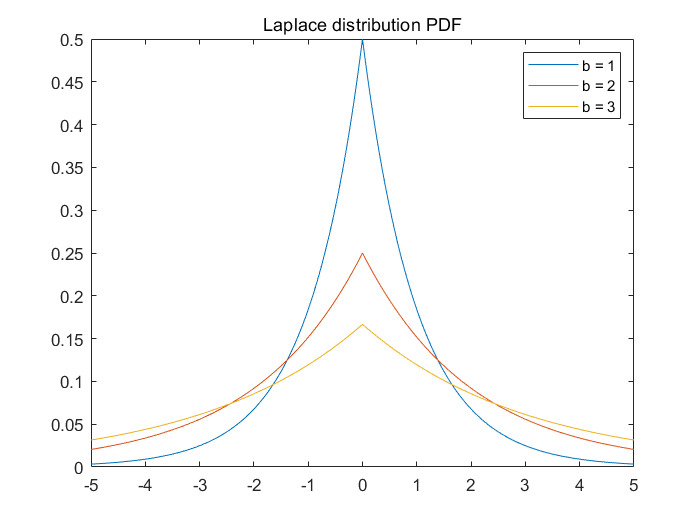
문제는 initialize할때 random하게 발생시킨 $\delta_j$들이 기반이 되는 growth rate k가 학습되는 걸 방해하면 안된다는 건데, 아까 언급한 Sparce하게 initializing을 한다는 개념이 이를 상쇄해 준다. 즉 델타들을 듬성듬성하게 초기화 해놓고, 초기의 tau값을 0에 가깝게 만들면 piecewise(조각단위)함수가 아닌 하나의 로지스틱이나 선형함수꼴로 나오기 때문에 k의 학습 또한 방해받지 않는다는 것.
Trend Forecast Uncertainty
만약 모델이 단순하게 과거 데이터를 extrapolating하면 Trend의 기울기가 하나의 상수형태로 나올 것이다. 이렇게 해버리면 기존에 changepoints들을 정의하고 사용한 이유가 사라져버린다. 이에, 논문에서는 forecast trend에서의 불확실성(uncertainty)을 generative모델을 확장시키는 방법으로 추정하려고 하였다.
S개의 changepoints가 존재하는 과거 T시점의 데이터를 바탕으로, 각 rate change를 $\delta_j \sim Laplace(0,\tau)$로 정의한 다음에 fitting 시킨다. (이러면 $\tau$대신 과거 데이터의 분산으로부터 추정된 어떠한 다른 값으로 바뀌게 됨)
이러한 방식이 베이지안 프레임워크상에서는 $\tau$에 대한 계층적 사전확률을 이용해 사후확률을 예측하는 방법으로 구할 수 있지만 굉장히 복잡하기 때문에, 최대우도추정법과 rate scale 파라미터 $\lambda = \frac{1}{s} \sum_{j=1}^S |\delta_j| $를 이용하는 방법으로 Tau를 추정할 수 있다고 한다.
이렇게 추정된 Trend 모델을 미래에도 적용시키는 방법으로 미래의 rate 변화를 시뮬레이팅 하며, 미래의 changepoints들은 평균 빈도가 과거에 발생했던 changpoints의 평균 빈도와 같도록 랜덤하게 샘플링된다.

위의 수식을 보면 알 수 있듯, T-S/T의 확률로 0을 갖게 하고, S/T의 확률로 Lambda를 분산으로 갖는 델타를 생성하여 평균 빈도가 과거와 같아진다.
정리하자면 미래의 데이터에서도 같은 빈도로 growth rate가 변하는 이벤트가 발생할 것이며, 그 이벤트가 가져오는 성장률 변화의 크기 역시 미래에 동일할 것이라는 가정 하에 과거 데이터를 바탕으로 generation model을 최대우도 추정법으로 학습시키고, 이렇게 만들어진 generation 모델로 미래의 시뮬레이션을 돌려보고, 추정된 tau를 바탕으로 uncertainty interval(불확실성 구간)을 측정한다. (통계에서 99% 신뢰구간이랑 비슷한 개념)
이렇게 만들어진 uncertainty interval은 당연히 시뮬레이션을 기반으로 결정된 것이므로 실제 통계에서의 신뢰구간이랑은 거리가 멀지만, 오버피팅을 판단하는 지표로서 사용될 수 있다. Tau값이 증가할 수록 모델이 과거 데이터를 이용한 fitting을 진행하는 데에 유동성이 증가하기 때문에 당연히 training error는 감소한다 (과거 시점을 그대로 따라가는 trend 그래프가 생성될 것). 하지만 이걸 이용해 인터벌을 생성해보면 매우 넓은 uncertainty intervals를 갖게 된다. (과거 데이터의 분산을 이용해 tau를 추정하기 때문에, 과거 데이터의 분산을 모조리 따라가는 모델로 시뮬레이션을 돌리면 당연히 tau값이 크므로 interval이 커진다.)
Seasonality
Prophet에서는 '푸리에 급수'*를 이용해 다양한 period에 유동적인 모델을 구축한다. P를 period라고 했을 때, 패키지에서는 연 단위 계절성 데이터에는 P = 365.25로, 주 단위 계절성 데이터에는 P = 7로 설정하는 방법으로 seasonal effects를 아래와 같이 결정한다.
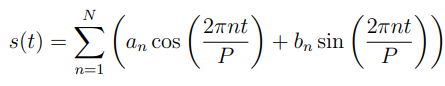
*푸리에 급수는 주기함수를 삼각함수의 가중치로 분해한 함수로, 굉장히 복잡한 파동을 단순한 파동의 조합으로 근사할 수 있다는 가정과 맞닿아 있다. 테일러 급수로 복잡한 함수를 근사하는 것과 비슷한 개념.
여기서 추정해야할 파라미터는 an과 bn으로, 패키지에서는 $\beta = [a_1, b_1, ... , a_N, b_N]^T$라는 2N개의 파라미터 벡터를 정의 한 뒤, P에 의해 결정되는 벡터 $X(t)$를 내적 하는 방식으로 계절성 함수 $s(t)$를 다시 정의한다.
예를 들어 연단위 계절성의 경우 $X(t)$는

이런 형식의 t에 대한 함수 벡터가 되고, Seasonal component $s(t)$는
$$ s(t) = X(t)\beta$$
가 된다. Trend에서의 방식처럼, $\beta \sim Normal(0,\sigma^2)$를 따르는 generating model을 이용해서 계절성을 smoothing 한다고 한다.
여기서 N이 trend에서의 $\delta_j$랑 비슷한 개념인데, 굉장히 연속적인 원래의 계절성을 N개의 constant만을 이용해 truncating 하는 것이기 때문에 N이 커지면 커질 수록 함수를 잘게 쪼개는 개념처럼 계절성의 적은 변화도 빠르게 잡을 수 있는 반면 overfitting의 위험도는 증가된다. 논문에서는 주로 연단위 계절성에는 N=10을 사용하고 주단위에는 N=3을 사용하는 것이 대부분의 문제에 잘 맞았다고 한다. 패키지에서는 이러한 파라미터를 AIC와 같은 지표를 이용해 자동적으로 결정한다.
Holidays and Events
휴일이나 이벤트는 trend나 계절성으로는 커버되지 않는 경우가 대부분이다. 예를 들어 음력을 기준으로 결정되는 휴일들이나, 미국에서의 슈퍼볼 경기일 등이 될 수 있겠다.
Prophet에서는 전 세계의 모든 holidays를 Table형태로 정리해 놓고

해당 time index t가 이러한 holiday 집합에 속하는지 아닌지를 결정하는 indicating vector Z(t)를 아래와 같이 정의한 다음,

학습되는 파라미터 kappa를 곱해주는 방식으로 holiday component를 정의한다.

여기서도 마찬가지로 사전확률 $\kappa \sim Normal(0,v^2)$을 사용한다.
또한 휴일 당일 뿐만아니라 추석과 같은 경우 그 주 자체가 특별한 날이 될 수도 있으므로, window 파라미터를 추가하여 휴일 당일 주변 날짜 또한 고려할 수 있도록 모델을 구성했다고 한다.
Model fitting
직전에 위에서 사용한 Dataset에 prophet을 fitting 한 결과이다. 각 예측은 예측일자 직전까지만 학습 된 상태이다. 다른 모델에서 발생했던 문제들을 거의 해결했음을 확인할 수 있다. holiday(end of the year)에 발생하는 dip 현상에 overeact하지 않았으나 조금 overfit 된 형태를 보이고 마지막 부분에서는 trend의 변화를 아직 학습하지 못한 형태를 보인다.

아래 그림은 전체 데이터에 대해 학습하고 fitting 한 결과로, 데이터를 전체 범위로 변경해서인지 마지막 부분의 Trend 변화 역시 반영된 형태를 보여준다.
아래 그림은 각 함수별 decompose 된 형태를 보여준다. 이 Visualization을 바탕으로 분석가들이 insight를 얻기 용이할 것이라고 논문에서는 언급하였다.

Regularization Factor들을 단순히 과거데이터를 이용해 추정하는 방식만으로는 충분하지 않은 경우가 더러 있어, 패키지에서는 대부분의 forecasting 모델에 적합한 Default 값들을 미리 설정해놓고 파라미터가 최적화 되어야 하는 상황이 발생하면, 이를 조정한다고 한다.
Analyst-in-the-Loop Modeling
분석가들이 모델을 변경할 수 있는 부분들은 다음과 같다.
- Capacites : 외부로부터의 정보 Ex) 시장의 크기 등을 이용해 capacity를 특정할 수 있다.
- Changepoints: 알고있는 날짜의 chagepoints들을 직접 입력할 수 있다.
- Holidays and seasonality: 지역이나 제품 특징 등에 따라 도메인에 대해 잘 아는 분석가가 매출 등에 영향이 있는 휴일을 직접 입력할 수 있다.
- Smoothing parameters: Tau를 조정하는 방법으로, global하게 smooth 된 모델이나, local 하게 smoothing 된 모델을 선택 할 수 있다. 또, 계절성과 휴일을 조정하는 파라미터 $(\sigma, v)$는 모델에 얼마나 과거의 분산을 미래에 적용할지를 결정할 수 있다.
이전파트에서 보여준 시각화들은 이러한 파라미터를 Tweaking하는데에 좋은 지표가 될 수 있다. 예를 들어 changepoint중에 빠진 것이 있을 때, 이를 자동적으로 찾아준다던가, 계절성 특징이 제대로 드러나지 않을 때, $\sigma$를 크게 한다던가 등 통계적으로 잘 모르는 사람도 쉽게 조정할 수 있도록 구성되어있다.
하지만 분석가가 이러한 Tweaking을 사용하고 판단하기 위해서는 적절한 평가지표가 존재해야 한다.
Use of Baseline Forecasts
논문의 해당 섹션에서는 수동적인 인간의 개입이 필요한 부분을 분석가에게 알려주고, 모델의 performance 평가를 자동화 하기 위한 방법을 다룬다. 하지만 수학적인 증명등을 바탕으로 내용이 구성된 것은 아니고, 중간 중간 in practice 즉 실제 적용 결과 이런게 좋더라 식으로 방법론을 선택했다고 한다.
예측 절차를 평가하는 데에 있어서, 가장 중요한 것은, 다양한 베이스라인 집합(다른 모델들)과 비교해 보는 것인데, 논문에서는 이러한 비교절차를 위에서 언급했던 arima, ets 등과 같은, 강한 가정을 바탕으로 한 간단한 모델이지만 실제 적용 했을 때 효과가 좋은 것들과 비교하는 방식을 택했다고 한다.
Modeling Forecast Accuracy
주로 기업에서 사용하는 예측은 특정 Horizon H를 바탕으로 진행하는 경우가 많다. 예를 들면 월별 H=30, 분기별 H=90, 반기별 H=180, 연별 H=365 등. 따라서 Forecasting 정확도를 측정하는데에 특정한 time horizon을 고려한 예측 성능 평가를 진행하는 것을 가장 주요한 기준으로 잡았다. $\hat{y}(t|T)$를 T 시점들의 historical information을 고려한 t시점의 예측이라고 가정했을 때, 예측 error $d(y, y')$은 mean absolute error와 같은 error metrics라고 하자. 그럼 $h \in(0,H]$ period에 대한 예측 정확도를 다음과 같이 표시할 수 있다.

이 정확도를 추정하고, h에 따라 이게 어떻게 변하는지를 확인하기 위해서, 에러 term에 대한 parametric model을 특정하고 이를 통해 데이터로부터 파라미터를 추정하는 방식이 사용된다.
예를 들어, AR(1) 모델을 사용하고 있다고 하자. $y(t) = \alpha + \beta y(t-1) + v(t)$ 여기서 에러 텀인 $v(t) \sim Normal(0, \sigma^2_v)$라고 가정하고, 데이터를 통해 $\sigma^2_v$를 추정한다.
그런 이후에는 추정된 에러텀을 가진 모델을 이용해 시뮬레이션을 돌리거나, analytic expression을 이용해 에러의 기댓값을 뽑아낼 수 있다. 그런데 이런식의 방법은 error에대한 정확한 추정치는 근사할 수 있을 지 몰라도 실제로 사용하기에는 어려움이 있다. (에초에 에러텀이 정규분포를 따른다는 가정 자체가 틀린 경우가 대부분)
따라서 논문에서는 위와 같이 파라미터를 추정하는 방식이 아닌, non parametric 접근 방식을 이용해 에러에 대한 기댓값을 추정할 수 있는 방식을 사용한다. cross validation에서 error를 추정하는 방식과 마찬가지로, 과거 데이터의 예측 집합을 이용해, 다른 예측 horizon h에 대한 expected error를 얻어낼 수 있는 모델을 학습시킨다.

이 모델은 유동적이면서도 몇 개의 가정들을 만족시킬 수 있어야 한다. 먼저 위와 같은 함수가 h 시점만큼 지역적으로 smooth 해야한다 (예측 오류가 발생했을 때, 해당 시점의 오류는 주변 시점에서의 오류와 유사할 것이므로). 두 번째로 function이 약하게 h 시점동안 증가해야한다. (어떻게 보면 당연한 가정이다. 시점 t=1에서 바로 다음 시점을 예측했을 때의 오차보다 다다음 시점의 예측 오차가 클 것이므로) 이 가정의 경우 모든 예측 모델에서 충족될 필요는 없다. 실제로는 error curve에 대해 local regression이나 isotonic regression 등을 사용한다고 한다. (결국 무슨 분포를 따른다는 가정은 충족되기 어려우니까 파라미터를 이용하지말고, 과거데이터를 통해 학습된 시계열 모델의 h시점의 예측을 시뮬레이션한 뒤. 나온 에러 평균 자체를 regression으로 학습 시키고 이 함수 자체를 모델링이 잘 되었는지 판단하는 지표로 사용한다는 얘기)
함수를 fit하기 위해 필요한 과거시점의 예측 데이터를 만들어 내기 위해 논문에서는 simulated historical forecasts라는 것을 사용한다고 한다.
Simulated Historical Forecasts
함수 fitting을 위해 simulated historical forecasts(SHFs)는 과거 데이터를 이용해 다양한 cutoff point를 선정하여 K개의 예측을 생산하고 total error를 계산한다.
이전에 등장했던 이 그림이 SHF의 하나의 예시인데, 특정 시점에서 h horizon에대한 예측을 수행했을 때 이를 그림으로 그린것이 아래 그림이다. 예를 들어 2014년 초에 반기의 예측을 진행한 것이 아래그림 첫 번째 예측 결과라고 할 수 있다.

당연히 h시점에 대한 total error 또한 구할 수 있다. 이제 이 예측 시점 T를 다양하게 바꾸고, h를 다양하게 변경해 줌으로서 이에 대한 Expectation값을 추정하는 함수를 fitting 하는 것이 prophet에서 택한 방법론이라고 할 수 있겠다.
이런 방법론을 사용하기 위한 두 가지 유의해야 할 점이 있다. 시뮬레이션을 많이 진행할 수록, error의 추정치들이 점점 correlated된다. 극단적으로 매일 마다 simulation을 진행하면 예측되는 에러값이 거의 유사해져서 거의 같게 된다. 만약 시뮬레이션을 너무 적게 돌리면 모델 선택에 필요한 충분한 정보를 제공하지 못하게 된다. 휴리스틱한 측면에서 만약 예측을 H 시점만큼 진행하면 2/H주기마다 시뮬레이션을 돌린다고 한다.
두 번째로, 데이터가 추가될 수록 forecasting 방법론이 더 잘 혹은 덜 잘 수행할 수 있다. 과거데이터 시점이 길어지게 되면 모델이 제대로 특정되지 않았거나 과거에 너무 오버핏된 경우 더 안 좋은 예측을 내놓을 수 있는데, 예를 들어 Sample 평균으로 trend를 예측하는 것이 있겠다.

위 그림은 autoarima, ets, prophet 등 의 모델들에 대해 위의 함수 $\xi(h)$를 fitting 한 결과이다. (distance metric으로는 MAPE를 사용하였다.) 추정된 함수를 살펴보면 다양한 forecast horizon에서 prophet이 우수한 성과를 거둔 것을 확인할 수 있다.
SHFs의 장점이 위 그림에서 드러나는데, horizon 크기에 따른 평균 error term에 대한 함수자체를 fitting해서 보여줌으로서 어떤 방식이 다양한 예측 horizon에서 우수한지를 한번에 시각화해서 확인할 수 있다.
또 SHFs를 사용하면 forecast에 문제가 생겼을 때, 자동적으로 분석가에게 이를 인지시켜 줄 수 있다.
- 만약 예측에 베이스라인 모델과 관련된 큰 오차가 발생하였을 때, 모델이 제대로 특정되지 않은 경우일 수 있다. 따라서 이를 통해 분석가가, trend나 seasonality를 조정할 수 있다.
- 만약 모든 방법론에서 특정 날짜에만 큰 오차가 발생한 경우, 이는 이상치가 영향을 주었을 가능성이 있다. 분석가는 이를 확인하고 제외시킬 수 있다.
- 만약 SHF 에러가 특정시점 이후부터 갑자기 증가하는 경우, 이는 데이터 생성 방식이 갑자기 변경되었다는 의미이다. 이를 보고 changepoint를 추가하거나 모델링을 구간을 나눠서 진행하는 경우 이 문제를 해결할 수 있다.
논문에서는 대부분의 경우 outlier 제거나 changepoint를 추가하는 방법으로 이를 조정할 수 있었다고 한다.
'데이터 과학 스터디 > 논문 리뷰' 카테고리의 다른 글
| [Pre-training of Deep Bidirectional Transformers for Language Understanding] BERT 논문 리뷰 (1) | 2023.02.16 |
|---|---|
| [NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE] Attention 논문 리뷰 (0) | 2023.02.16 |
| [Word2Vec] CBOW, Skip-gram 논문 리뷰 (0) | 2023.01.31 |
| [Transformer: Attention Is All You Need] 논문리뷰 (0) | 2022.11.09 |
| [Generative Adversarial Nets] 논문 리뷰 (1) | 2022.09.28 |



