*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.

Week 3-2에서는 단계 4 에서부터의 내용을 다룬다.
시계열 모형 추정방법
- 최소차승법 (least squares method): AR모형의 경우에만 사용 가능하고 일반적으로는 불가.
- 비선형 최소차승법 (nonlinear least squares method): ARMA 모형에 적용 가능하나 주로 최우추정법을 사용한다.
- 최우추정법 (maximum likelihood estimation)
최우추정법
- IDEA: 오차항이 서로 독립인 정규분포를 따르므로 우도함수 (likelihood function)를 유도해 이를 최대로하는 모형 계수들을 추정한다. 하지만 ARMA 모델의 경우 정확한 우도함수 도출이 어렵고 초기치에 대한 가정이 필요하다.
이에 여기서 우도함수는 세가지로 분류할 수 있다.
- 정확한 우도함수
- 조건 있는 우도함수 : 임의로 초기치를 가정하고 사용
- 조건 없는 우도함수 : 과거의 초기치를 후방예측(backcasting)하여 사용
정확한 우도함수
먼저 우도함수와 최우추정법이 무엇인지 정리하고 진행해보자.
정규분포를 따르는 관측치에 대해 각 관측치는 서로 독립이므로 joint distribution을 pdf의 곱으로 표현할 수 있다.

위의 복잡해 보이는 식은 정규분포 pdf의 곱을 의미한다.
이 복잡한 식의 $x_i$ 즉 관측데이터를 대입하게되면 결국 상수의 꼴이 되어 이를 모수인 평균과 표준편차 제곱의 함수로 간주할 수 있고 이러한 형태를 우도함수 $(L)$라고 하며, 이를 최대로하는 모수를 추정하는 방법을 최우추정법이라고 한다.

우도함수에 $\log$를 씌우게 되면 함수의 $\exp$부분을 뽑아낼 수 있어 계산을 용이하기 위해 로그우도함수를 주로 사용한다.
조건있는/없는 우도함수
문제는 우리가 다루는 관측치$(Z_1 \sim Z_n)$은 서로 독립이 아니다. (즉 직접적인 우도함수의 구성이 어려움)
이에 대신 백색잡음$(a_1 \sim a_n)$이 서로 독립임을 활용해 이에 대한 우도함수를 구성한다.

이를 위해 각 관측치를 이용해서 각 시점의 $a_t$를 모두 계산해야 한다. AR(1)을 예시로 들자면, $a_t$를 좌항으로 넘기고 나머지를 정리해 보면 아래 식과 같은데, $a_t$는 $a_1$을 기점으로 해서 연쇄적으로 구해진다.
문제는 $Z_0$는 주어진 관측치$(Z_1 \sim Z_n)$에 존재하지 않는 변수이므로 $a_1$을 구할 수가 없다.
따라서 이를 특정한 가정에 따라 초기화하고, 이를 이용해 $a_1$을 계산해야 한다.

여기서 초기치 처리 방법을 기준으로 조건있는/없는 우도함수로 나뉘어진다.
조건있는 우도함수
먼저 조건있는 우도함수의 경우를 ARMA(p,q)로 확장시켜 살펴보자.
ARMA(p, q)로 확장하게 되면, $a_1$을 구하기 위해 필요한 변수가 훨씬 증가된다. 아래 그림 (ARMA p,q 모형에서$ a_1, a_2 ... a_n$ 산출) 부분을 살펴보면 $a_1$을 구하기 위해 $a_0, a_{1-q}, z_0$등 관측되지 않은 값들이 필요함을 확인할 수 있다.

일반적으로는 $a$ 즉 백색잡음의 경우 0으로 가정하고, 과거의 관측값들은 $Z$의 평균으로 가정한다고 한다.
이렇게 초기화를 진행하고 나면, 로그 우도함수가 아래와 같은 형태로 표시된다. 우도함수에서 마지막 $\theta $항을 제외하면 모두 fix된 숫자이므로, 로그 우도함수를 최대화 하는 것은 마지막 항을 최소화 하는 것과 같게 된다.
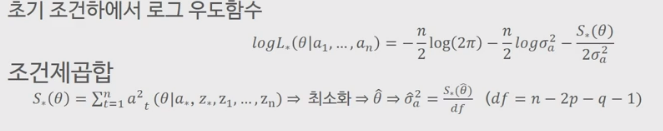
결국 이 마지막 항을 최소화 하는 $\theta_1, \theta_q, \phi_1, \phi_p$ 등을 찾는 것이 목적이 된다.
실제 예를 통해 살펴보면,
최우 추정법으로 $\phi_1$을 추정하기 위해서 $\phi$ 값을 여러가지 시도해 보고 제곱합을 최소화 시키는 것을 찾는 방식으로 계산된다. 아래 표를 보면 0.2, 0.4를 넣어서 제곱합을 구해 비교하게 된다. 이 과정은 최적화 알고리즘을 통해 진행된다.

조건없는 우도함수
조건없는 우도함수의 경우 예측을 통해 진행하게 되는데, 여기서의 중요한 아이디어는 "일반적으로 과거를 통해 미래를 예측하듯, 시계열 데이터를 역으로 생각해 미래를 통해 과거를 예측하자"이다. 이를 후방예측(Backcasting)이라고 한다.
예를 들면 $Z_t, Z_{t-1}$ -> $Z_{t+1}, Z_{t}$ 로 보는 것이다.

마찬가지로 자세한 과정은 소프트웨어로 계산된다.
아래 테이블을 보면 $Z_1, Z_2$ 등을 소프트웨어를 통해 계산한 뒤, 이를 이용해 제곱합을 최소화 시키는 $\phi$와 $\theta$를 계산한다.

단계 4:
이전 Week 3-1의 나일강 유량 데이터 예제에서 우리는 AR(1)이나 AR(2)모형일 것이라고 판단을 진행했다. 이를 AR(2)를 따른다고 하면, 이를 이용해 조건있는/없는 우도함수를 maximize하는 $c, \phi_1, \phi_2$를 찾는 것이 단계4가 되겠다.
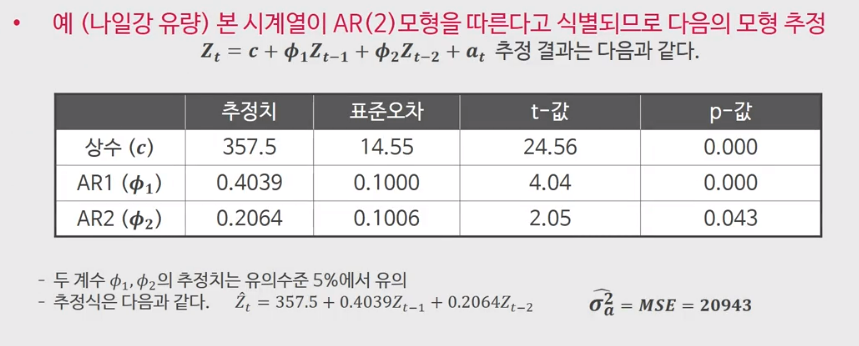
단계 5:
모형의 검증
가장 처음 시점에 $a_t$들이 백색잡음이라고 가정했으므로 이에대한 정규성과 등분산성에 대한 검증이 필요하다.
정규성은 일반적으로 정규확률도표를 활용하며, 등분산과 패턴유무는 산점도(Scatter plot)을 활용한다.
잔차가 랜덤성을 가지면 모든 시차에 대해 ACF/PACF가 0이 되므로 이를 확인해야 하고, 이 외에도 여러 검정방법이 있다. (white 노이즈 이므로 당연히 랜덤성을 가져야 한다.)

다시 나일강 예시로 돌아가보자.
정규성
먼저 정규확률도(q-q plot)을 살펴보면 직선의 형태를 어느 정도 띔을 확인할 수 있다. -> 정규성을 띈다
두번째로 히스토그램 역시 0을 기준으로 정규분포의 형태를 띈다는 것을 확인할 수 있다. -> 정규성을 띈다.
(두 과정 모두 반대는 정규성을 띄지 않음의 근거가 될 수 있다.)
잔차의 산점도 역시 특정한 패턴을 띄는 것으로 보이지 않아 모형이 적합하다고 할 수 있다.

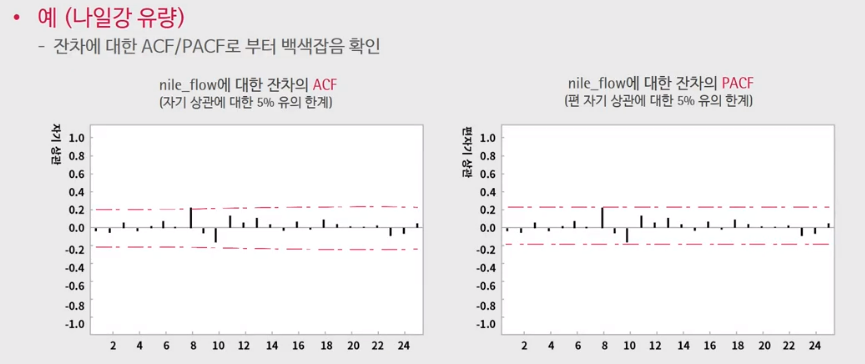
이번에는 ACF/PACF를 보면 모든 시점에서 유의한계 내에 있음(0이다)을 확인할 수 있다. -> Random성 확인
마지막으로 포트만토 검정 결과를 살펴보자.

포트만토 검정에서 H0: 자기 상관이 없다 인데 p 값이 크므로 이를 기각하지 못한다. 즉 자기 상관이 없다는 의미이다.
단계 5:의 과정을 거쳐 AR(2) 모형이 나일강 유량 데이터에 적합함을 결론지을 수 있다.
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week4-1 비정상적 시계열 모형화를 위한 ARIMA 모형 (0) | 2023.03.22 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-3 최소평균오차 기반의 ARMA 모형 예측치 유도 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-1 ARMA모형의 식별: 시차판정 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-4 ARMA모형 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-3 AR모형 및 MA모형의 표현 및 성질 규명 (0) | 2023.03.15 |



