*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
모형의 식별, 추정 및 검증과정
크게 5가지 단계로 구성된다.
단계 1의 경우는 현재 과정과 다른 내용이라 이번 강의에서 다루지 않았다.

단계 2: 표본 ACF와 PACF 산출
지금까지는 표본이 아니라 이론적인 ACF, PACF에 대해 알아보았다.
실제 데이터에 적용하기 위해서는 아래와 같이 실제데이터를 바탕으로 ACF와 PACF를 산출해야 한다.


단계 3: 이론적 ACF, PACF를 바탕으로 표본 ACF, PACF와 비교해 ARMA 차수를 구한다.
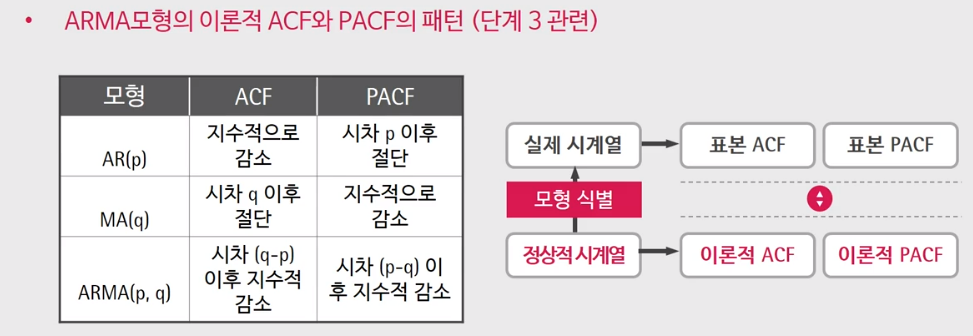
단계 1~3을 두 가지 예시를 통해 직접 따라가 보자
Example 1)
단계 1: 정상성 확인 -> 평균이 크게 변동하지 않고 유지되고 있으며 계절성 또한 보이지 않는다. 정상성을 띌 것 같으나, ACF를 통한 추가 확인이 필요해 보인다.

단계 2: 표본 ACF, PACF를 구하고 ACF를 확인해보면 급격히 떨어진다는 것을 확인할 수 있다. -> 정상성이 확인됨.

단계 3: 표본 ACF의 경우 지수적으로 감소, PACF의 경우 시차 1 혹은 2를 제외하고는 5% 유의한계 내에 존재한다. (즉 유의하지 않은 상관관계, 0을 의미) 따라서 절단패턴을 띈다고 볼 수 있다. -> AR(1) or AR(2)모형이다.

Example 2)
단계 1: 먼저 그래프의 형태를 보면, 평균이 꾸준히 변하고 있으므로 정상성이 아님을 짐작 할 수 있다.

단계 2: 표본을 이용해 ACF를 그려보면 (위 오른쪽 그림) ACF가 급격하게 감소하는 것이 아니라 서서히 감소함을 확인할 수 있다. -> 비정상성 확인.
따라서 단계 1로 돌아가 정상성을 만족시켜줘야 한다.
단계 1: 데이터를 차분(Differencing)하여 정상적 시계열로 변환하였다.

단계 2: 표본 ACF를 확인해 보면 ACF가 빠르게 감소함을 확인할 수 있다.(정상성 확인 완료)
단계 3: ACF의 경우 시차 1을 제외하고는 유의한계 내에 plot 되었고, PACF의 경우 지수적으로 감소하므로 MA(1) 모형이다.

강의에서는 그래프를 이용한 단계 3을 너무나 당연한 듯이 설명해 주셨으나, 나의 경우 ACF, PACF가 모두 유의한계선 내로 들어갈 때, 어떤 것을 지수적인 감소로 봐야하고, 절단패턴으로 봐야하는지 파악하는 것이 어려웠다. 다만 굳이 위의 두 예시에서 힌트를 찾아보자면,
지수적 감소의 경우 유의한계선 내에서도 꾸준히 감소하는 모습을 보여준다면
절단 패턴의 경우 유의한계선 내에서 크기가 들쑥날쑥 하는 형태를 띈다.
둘다 아니라면 ACF, PACF 중 어떤 것이 상대적으로 절단패턴에 가까운지를 확인하는 것이 용이할 것 같다.
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-3 최소평균오차 기반의 ARMA 모형 예측치 유도 (0) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-2 ARMA모형의 파라미터 추정을 위한 최우추정법 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-4 ARMA모형 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-3 AR모형 및 MA모형의 표현 및 성질 규명 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-2 편자기상관함수, AR/MA 표현방식, 후향연산자 (0) | 2023.03.15 |



