*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
ARMA 모형
두 모형 AR, MA의 복합 형태이므로, 정상성 조건과 가역성 조건이 동시에 필요하다.

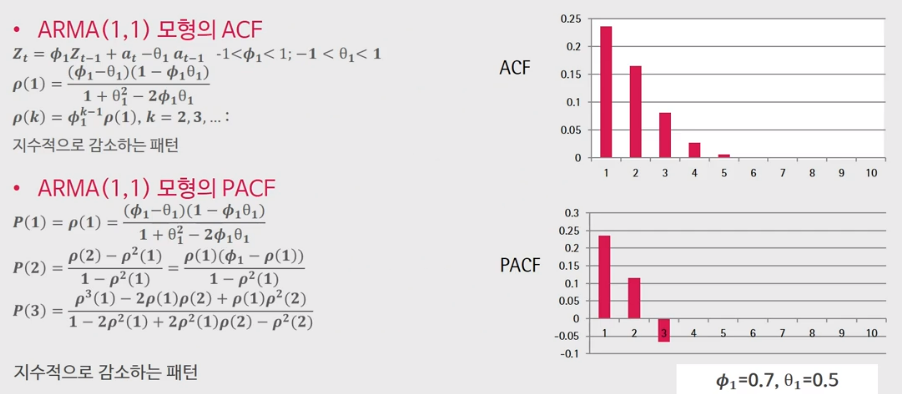
ARMA(1,1)모형의 ACF, PACF
ACF의 경우 $\rho (1)$만 구하면 $\phi $를 계속 곱해주는 형태여서 지수적으로 감소하는 패턴이다.
PACF 역시 복잡하지만 계산시 지수적으로 감소하는 패턴을 띈다.
ARMA(p,q)모형의 ACF, PACF
이번에는 일반화된 ARMA(p,q) 모형을 확인해보자.
아래의 성질은 ARMA 모델을 구상할 때, ACF와 PACF를 바탕으로 가장 적절한 $p$와 $q$를 선택하는 데에 도움을 준다.
*0으로 떨어진다는 의미는 지수적으로 감소한다는 의미를 포함하고 있다.

예시를 통해 확인해보자.
먼저 ARMA(1,3)을 보면 $q$가 $p$보다 크므로,
ACF : $q-p = 2$만큼 별개 값을 갖고, 이후에 지수적으로 감소한다.
PACF : 처음부터 지수적으로 감소한다.
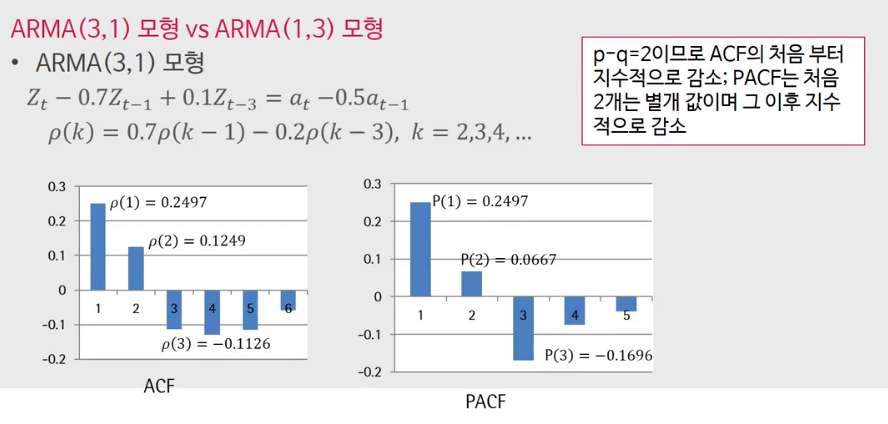
이번에는 ARMA(3,1)을 보면 $p$가 $q$보다 크므로,
ACF: 처음부터 지수적으로 감소
PACF: 시차 $p-q = 2$만큼 별개 값을 갖고, 이후에 지수적으로 감소한다.

AR, MA, ARMA 모형 모두를 정리해 보면 아래와 같다.

'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-2 ARMA모형의 파라미터 추정을 위한 최우추정법 (0) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-1 ARMA모형의 식별: 시차판정 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-3 AR모형 및 MA모형의 표현 및 성질 규명 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-2 편자기상관함수, AR/MA 표현방식, 후향연산자 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |



