*이 글은 실전 시계열 분석 책을 기반으로 작성되었습니다.

시계열 데이터의 전처리 Flow
일변량 시계열 vs 다변량 시계열
- 일변량 (univariate) : 시간에 대해 측정된 변수가 하나인 경우
- 다변량 (multivariate) : 시간에 대해 측정된 변수가 여러개인 경우
저자는 시간에 따라 정렬된 데이터셋 (EX: Kaggle과 같은 대회용 데이터셋) 이 아니라, 시계열로 주어지지는 않았으나, Time stamp, "시간" 은 없지만 시간을 대체할 수 있는 데이터 혹은 물리적 흔적이 남은 데이터 셋을 일컬어 발견된 시계열 found time series라고 명칭한다.
2 장에서는 발견된 시계열을 어떻게 전처리 하는지를 예제와 함께 다룬다.
먼저 예제를 통해 큰 흐름을 살펴보자.
발견된 시계열의 예시로, 기업에서 사용하는 SQL 데이터셋 예제이다.
| 회원 ID | 가입 연도 | 회원 상태 |
| 1 | 2017 | gold |
| 2 | 2018 | silver |
| 3 | 2016 | inactive |
| 회원 ID | 주 | 열어본 이메일 개수 |
| 2 | 2017-01-08 | 3 |
| 2 | 2017-01-15 | 2 |
| 1 | 2017-01-15 | 1 |
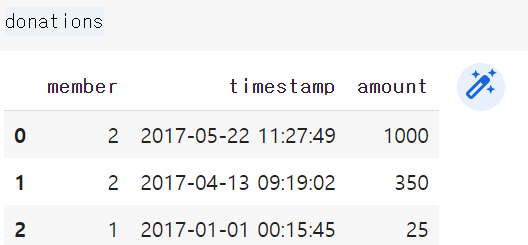
| 회원 ID | 타임스탬프 | 기부금 |
| 2 | 2017-05-22 11:27:49 | 1,000 |
| 2 | 2017-04-13 09:19:02 | 350 |
| 1 | 2017-01-01 00:15:45 | 25 |
이를 어떻게 하면 시계열 분석에 합리적인 형태로 데이터를 구성할 수 있을까?
먼저 데이터에서 시간축을 고려해보자.
각 표는 다음과 같은 기준으로 시간을 구분한다.
- 연간 회원 상태
- 이메일 열람에 대한 주간 누적 기록
- 기부가 이뤄진 순간의 타임스탬프
이 중 연간 회원 상태의 경우, 데이터가 의미하는 바가 정확히 어떤 것인지 확인이 필요하다.
회원 상태가 "연간"으로 주어져 있는지. ex: 회원 1이 2017 년에는 gold, 2018 년에는 silver...
혹은 "최근" 상태로 주어져 있는지. ex: 회원 1이 데이터가 수집된 "현재" 기준 gold인지
혹은 데이터를 과거 2018년에 입력하고 갱신이 안되어 있는 상태인지...
이를 위해 저자는 다음과 같은 python 코드를 이용해 먼저 맴버ID 기준 year와 status의 개수를 count() 한 뒤, 다시 status 기준으로 묶고 count 하는 방식으로 각 맴버가 하나의 Year 기준으로 되어 있는지를 확인한다.
YearJoined.groupby('memberID').count().groupby('memberStats').count()가장 최근 상태인 경우



회원별 연간 상태인 경우



책에서는 결과 값이 회원수 = 1000과 일치하므로 (위 그림처럼 결과 값이 여러개의 row로 나눠지지 않으므로) 가장 최근 데이터이거나, '언젠가' 입력된 데이터임을 확인했다.
이 경우 위에서 사용한 df를 시계열 모델에 입력해도 될까? -> X
과거의 데이터 분석에 '현재 상태'가 고려될 수 있는 "사전관찰(look-ahead)" 문제가 생길 수 있음.
이번에는 두 번째 테이블을 살펴보자. '주' 라는 column을 살펴보면 이게 어떤 방식으로 주(week)를 시간(time)으로 표현했는지 확인해 봐야한다.
('2017-01-08', '2017-01-15' 를 미루어 보아 주가 시작하는 날짜 기준인 것 같으나, 일요일 시작인지, 월요일 시작인지도 모르고 하물며 '2017-01-01'을 한 주의 시작으로 설정했을 수도 있다. )
또한 어떤 주에 Null이 있는지도 살펴보아야 한다. 특정 회원이 한번도 이메일을 열람하지 않은 주는 당연히 존재할 수 밖에 없는데, 이를 이메일 열람횟수 = 0으로 처리했는지, 아니면 그냥 데이터를 공백으로 넣었는지도 확인해 봐야 한다.
저자는 맴버 한명의 데이터에 빠진 주(week)값이 있는지 확인하는 방법으로 Null 유무를 확인한다.
emails[emails.member == 2]해당 코드로 ID=2인 멤버의 모든 데이터를 불러와서 빠진 주가 있는지 찾아본다. 책에서는 2017-12-04 부터 2018-03-05까지 데이터 중 2017-12-18 이후의 데이터가 아예 존재하지 않는 것을 확인한다. -> 열람 횟수 0으로 빈 부분을 채운게 아니라 그냥 공백으로 두었다는 것을 확인함.
그냥 이대로 데이터를 사용하게 되면, 서로 다른 Member들에 대한 데이터를 시간 순으로 정렬할 수 없음 (맴버마다 다르게 '주' 데이터가 공백으로 있으므로)
빠진 week 데이터에 열람횟수 0을 기입하는 방식으로 Null을 표현할 수 있도록 전처리 한다.
all_email = emails.set_index(['week','member']).reindex(complete_idx, fill_value=0).reset_index()
all_emails.columns = ['week', 'member', 'EmailsOpened']
#column 이름 지정상세한 동작은 아래와 같이 진행된다.
1. MultiIndex.from_product 함수를 이용해서 outer join된 index행렬을 만든다.
2. 기존 email 데이터 프레임의 인덱스를 기존 column인 'week'와 'member'로 대체한다.


3. 현재 인덱스를 아까 생성한 outer join 인덱스 행렬로 교체하고, 해당되지 않는 value는 0으로 대체한다.
4. 인덱스 초기화로 인덱스를 다시 column으로 반환한다.
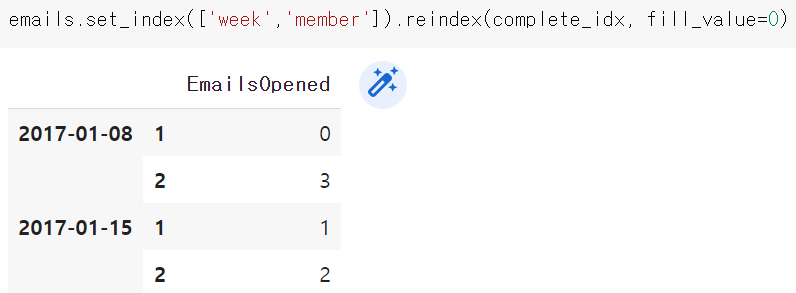
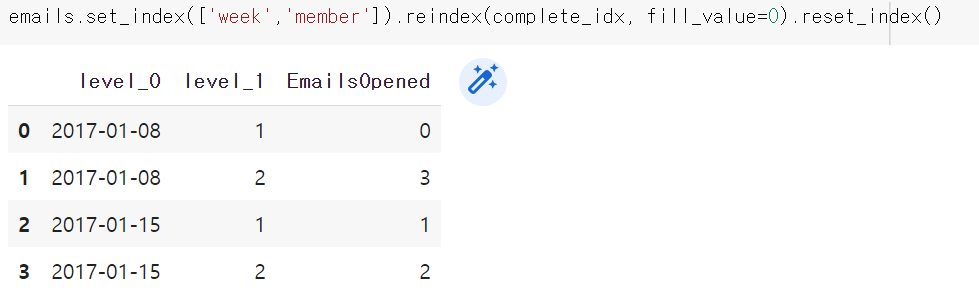
하지만 이렇게 데이터 프레임을 구성하면 특정 회원이 회원가입을 하기 전임에도 데이터가 0으로서 존재하는 문제가 생긴다.
아래와 같은 코드로 회원이 처음으로 email을 읽은 시기 이전의 데이터와 마지막으로 읽고 난 이후의 데이터를 삭제하는 방법으로 이 문제를 해결할 수 있다.
cutoff_dates = emails.groupby('member').week.agg(['min','max']).reset_index()
for _, row in cutoff_dates.iterrows():
member = row['member']
start_date = row['min']
end_date = row['max']
all_emails.drop(all_emails[all_emails.member == member][all_emails.week<start_date].index, inplace=True)
all_emails.drop(all_emails[all_emails.member == member][all_emails.week>end_date].index, inplace=True)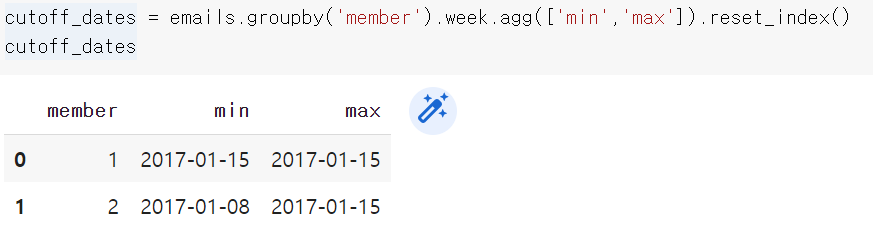
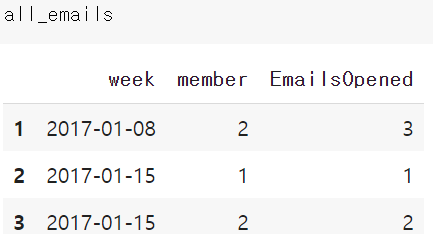
all emails 에서 member 1 EmailsOpend = 0 이었던 row가 삭제된다.
이전에 0으로 채운게 없어져서 roll back 된게 아니냐고 생각할 수 있지만, 적은 데이터 예제여서 그렇고, 실제로는 회원 기준 앞(회원가입 이전)과 뒤(마지막 이메일 열람 이후)만 제거하는 것이므로 week 정보는 모든 시간 정보를 포함하며 보관된다.
이메일 데이터 (2번째 table)와 기부금 데이터 (3번째 table)을 취합해보자.
- 연간 회원 상태
- 이메일 열람에 대한 주간 누적 기록 (2)
- 기부가 이뤄진 순간의 타임스탬프 (3)
실제로 기부를 한 주에 두 번 이상 하는 경우는 드물므로 Time stamp를 '주' 단위로 맞추면 합리적일 것이다.
저자는 다음과 같은 코드로 진행한다.
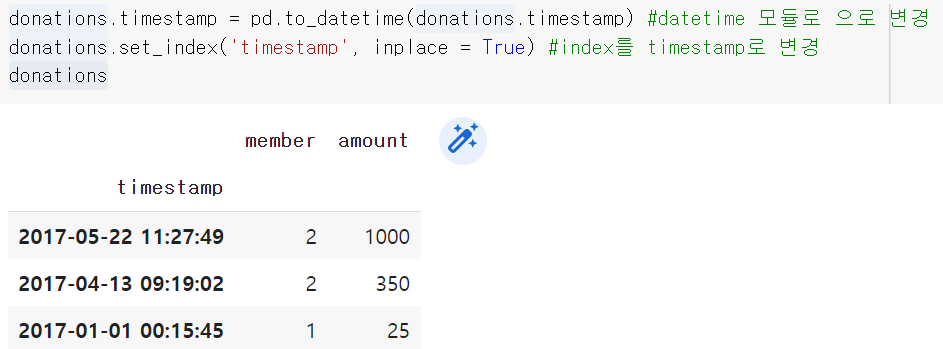
donations.timestamp = pd.to_datetime(donations.timestamp) #timestamp를 datetime 모듈로 변경
donations.set_index('timestamp', inplace = True) #index를 timestamp로 변경
agg_don = donations.groupby('member').apply(lambda df: df.amount.resample("W-MON").sum().dropna())마지막 코드가 조금 어려운데, resample 함수의 경우 datetime을 원하는 주기로 나누어 주는 함수로, 이 경우 Monday를 기준으로 datetime을 분리한다. 코드 실행 결과들은 아래와 같다.
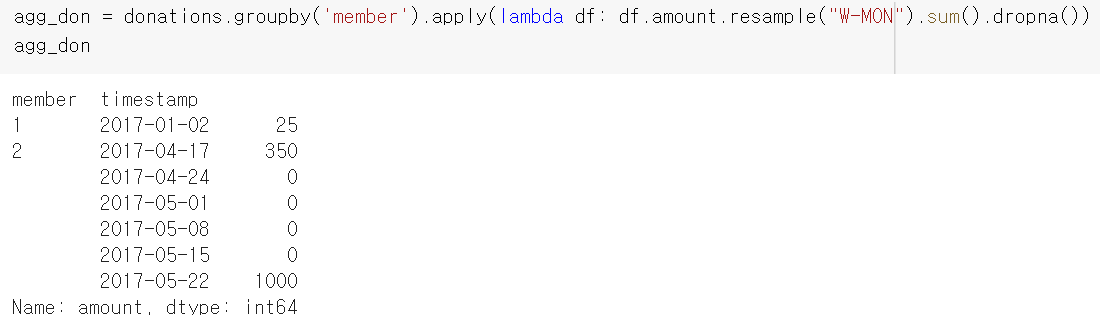
다음으로 두 테이블 데이터를 통합해보자.
코드는 아래와 같다.
agg_don = donations.groupby('member').apply(lambda df: df.amount.resample("W-MON").sum().dropna())
agg_donations = agg_don.reset_index()
merged_df = pd.DataFrame(data=[],columns = ['member','week','EmailsOpened','amount'])
for member, member_email in all_emails.groupby('member'):
member_donations = agg_donations[agg_donations.member == member] #email 데이터에서 꺼내온 member정보와 매칭되는 agg_donations 데이터프레임을 가져온다.
member_donations.set_index('timestamp', inplace = True)#index를 column인 timestamp로 변경
#member_email.set_index('week', inplace = True) #email table의 index를 week로 변경? 필요없는 코드인듯.
member_email = all_emails[all_emails.member == member] #for 문에서 꺼내온 member에 해당되는 all_emails의 데이터프레임을 가져온다.
member_email.sort_values('week').set_index('week') #week 정보에 따라 sort한다음 index를 week로 변경
df = pd.merge(member_email, member_donations, how = 'left', left_index = True, right_index = True)
df = df.fillna(0) #책 코드 오류인듯. 이렇게 해야 할당된다.
df['member'] = df.member_x
merged_df = merged_df.append(df.reset_index()[['member','week','EmailsOpened','amount']])책에 있는 코드가 잘못된 것 같아 수정하였다.
결과는 아래와 같다.
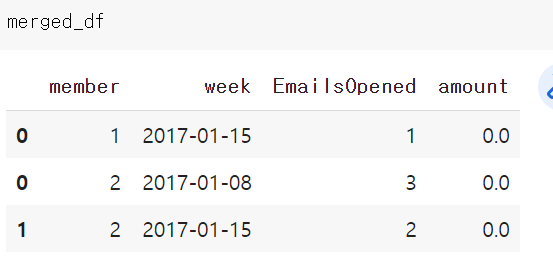
SQL에서는 굉장히 간단한 문법이나 파이썬에서는 생각보다 어렵다.
만약 얻어낸 merged_df에서 기부 내역을 한 주 뒤로 미루고 싶다면 다음과 같은 코드를 사용할 수 있다.
대부분 이전 데이터를 이용해서 target 변수를 예측하므로 타겟 변수 생성시 아래 코드를 이용하면 될 것이다.
df = merged_df[merged_df.member ==2]
df['target'] = df.amount.shift(1)
df = df.fillna(0)
df
지금까지 예제로 살펴본 내용을 정리해보면 이렇다.
- 해결하고자 하는 문제에 맞는 형태로 데이터의 간격을 교정한다. (Timestamp 데이터는 초단위 까지 주어짐. 이를 주 단위로 교정하였다.)
- 사전관찰을 피하기 위해 시간 파악이 불명확한 데이터를 사용하지 않았다. (연간 회원 상태 데이터의 경우 정확히 언제 데이터가 주어졌는지 확인이 어려워 사용하지 않았다.)
- 아무일이 없었더라도 관련된 모든 기간을 기록하자. 0일지라도 유용한 정보이다. (Email 데이터 혹은 Donation 데이터에서 아무일도 일어나지 않았으나, 주 단위 설정을 하면서 빈 Null 값은 0으로 대체하였다.)
- 사전관찰을 피하기 위해 아직 알면 안되는 정보를 배제하는 방법을 이해하였다. (shift 함수로 타겟 변수의 경우 현재 정보를 고려하지 못하도록 하였다.)
Time Stamp Data의 고려할 점
Timestamp 데이터의 경우 시간과 요일 등 많은 특징을 얻어낼 수 있으므로 유용하나, 다음과 같은 문제들이 존재한다.
- 파일 생성 시기: 파일이 이동하면서 찍힌건지, 생성하면서 찍힌건지, 복사하면서 찍힌건지 알 수가 없다.
- 누군가 기입했을 경우: 음식 기록 앱에서 먹은 음식 정보를 즉각 기입이 아니라, 하루가 끝나고 기록했을 수도 있다.
- 시간 기준이 모호: 세계시간 기준인지, 특정 좌표에서의 기준(현지 시간)인지 등 확인이 어려움.
이런 경우 timestamp 에 대한 EDA를 진행하거나, 작성자에게 질문을 하거나 등의 방법으로 알아내야 한다.
*일반적으로 UTC(세계 협정 시간)으로 타임 스탬프를 다루는 것이 가장 좋다.
시간 규모(단위)에 따라서도 오차가 생길 가능성을 고려해야한다.
사람이 기입하는 자료의 경우 '일주일 만에 기입' vs '1년 만에 기입'이 당연히 다를 수 밖에 없다. (인지 편향 등으로 인해)
이를 해결하기 위해 개별적으로 다루기 보다는 평균을 사용하는 등 Smoothing을 진행하는 것이 좋다.
데이터 정리
데이터 전처리에 고려해야할 문제는 다음과 같다.
- 결측치
- 시계열의 빈도 (시간 단위)
- 데이터 Smoothing
- 데이터의 계절적 변동이나 Trend
- 의도치 않은 사전관찰 방지
1. 결측치
가장 크게 다음 3가지 방법이 있다.
- 대치법 (imputation) : 데이터셋 전체의 관측에 기반, 누락된 데이터를 채워 넣는 방법
- 보간법 (interpolation) : 대치법의 한 형태로 인접한 데이터를 사용하여 누락된 데이터를 추정하는 방법
- 영향받은 기간 삭제: 누락된 데이터의 기간을 완전히 사용하지 않는 방법
Forward fill : 누락된 값이 나타나기 직전의 값으로 누락된 값을 채운다.
Backward fill : 누락된 값 이후의 값으로 누락된 값을 채운다. (사전 관찰)
Moving Average(이동 평균법) : 누락이 발생하기 이전의 값들에 대한 평균으로 누락된 값을 채워 넣는다. 이 때, 반드시 산술 평균만 사용해야 하는 것은 아니며, Exponentially Weighted Moving Average(지수가중이동평균) 으로 최근 데이터에 더 많은 가중치를 줄 수 있고, Geometric mean(기하평균)은 일련의 데이터가 강한 상관관계를 가지고 시간이 지나면서 복합적인 값을 가지는 시계열에 유용하다.
보간법 : 전체 데이터를 기하학적으로 제한하여 누락된 데이터를 결정하는 방법. 선형 보간법은 누락된 데이터가 선형적인 일관성을 갖게끔 제한한다. (표현이 어려우나, 정리하면 [01일에 3, 02일에 Null, 03일에 5] 라는 자료가 있을 때 선형 보간법은 3+5/2 = 4를 02일에 넣는 것이다.) 다만 시스템에 선형적 혹은 다른 패턴이 존재한다는 가정이 필요하며, 사전관찰 문제가 필연적으로 발생한다.
2. 시계열의 빈도 (Upsampling and Downsampling)
서로 다른 빈도의 시계열 데이터 두개를 분석해야 하는 경우 빈도를 동일하게 맞춰 주어야 하기 때문에 필요한 작업이며 빈도 조정 종류에 따라 두 가지로 나뉜다.
Upsampling : 타임스탬프의 빈도를 늘이는 작업 (연 단위 데이터를 일 단위로 변경하는 것)
Upsampling을 해야하는 경우는 다음과 같다.
시계열이 불규칙적인 경우 (위에서 다룬 예제에서도 '주' 단위였는데 빠진 시간대가 존재해서 0값으로 빈도 조정했다.)
어떤 모델을 써야 하는데, Input 으로 더 낮은 빈도를 요구하는 경우
Downsampling : 타임스탬프의 빈도를 줄이는 작업 (시 분 초 까지 세세한 데이터를 '주' 단위로 바꾸는 것)
Downsampling을 해야하는 경우는 다음과 같다.
원본 데이터의 시간 단위가 지나치게 세세함 (Ex : 시간에 따른 키 성장을 보는데 초 단위로 잰 경우.)
계절 주기의 특정 부분에 집중하는 경우 (다른 시기 말고 1월에만 관심이 있는 경우)
더 낮은 빈도의 데이터에 맞추는 경우
*Pandas 의 resample 메서드를 사용하자.
3. 데이터 Smoothing
Smoothing 의 목적:
- 이상치 혹은 특이치 등의 noise 를 제거하기 위해
- Expectation 등 요약을 통해 데이터의 'feature'을 생성하기 위해서
- 간단한 예측을 진행
- 조금 더 깔끔한 시각화를 위해서
Smoothing의 예시로 지수평활이 있다.

간단하게 말하면 이전 데이터에 (1-alpha)를, 새롭게 들어온 데이터(현재 데이터)에 alpha를 곱해서 쌓아가는 방식이다. 즉 alpha가 클 수록 현제 데이터에, alpha가 작을 수록 과거 데이터에 가중치를 부여하는 방식.
* alpha 는 평활요인(Smoothing factor)라고도 불린다.
간단한 파이썬 코드는 다음과 같다.
import pandas as pd
#데이터 생성
air = pd.DataFrame([
['1949-01', 112],
['1949-02', 118],
['1949-03', 132],
['1949-04', 129],
['1949-05', 121],
['1949-06', 135],
['1949-07', 148],
['1949-08', 148],
['1949-09', 136],
['1949-10', 119],
['1949-11', 104],
], columns = ['Date','Passengers'])
air['Smooth.5'] = air.ewm(alpha=0.5).mean().Passengers
air['Smooth.1'] = air.ewm(alpha=0.9).mean().Passengers
air결과는 다음과 같다. 두 번째 Row 만 보더라도, alpha = 0.9인 Smooth.1이 더 현재 값에 가중치를 줬음을 확인할 수 있다.
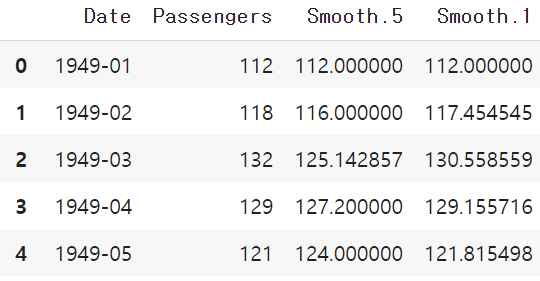
하지만 지수평활의 경우 장기적 추세에서 제대로 기능을 하지 못한다. 이를 보완하는 방법론은 아래와 같다.
홀트 방법(Holt's method) : 추세(Trend)를 가진 데이터에도 적용 가능
홀트-윈터스의 평활(Holt-winters smoothing) : 추세 뿐만 아니라 계절성이 있는 데이터에도 적용 가능.
이 외에도 다양한 방법론이 있다.
Kalman Filter : 변동성 및 측정 오차의 조합(Variance and bias)로 시계열 process를 모델링해 평활
Locally Estimated Scatterplot Smoothing(LOESS) : 지역적으로 데이터를 평활하는 비모수 방법론.
위 두 가지 방법론은 사전관측 문제가 존재한다.
4. 데이터의 계절적 변동이나 Trend
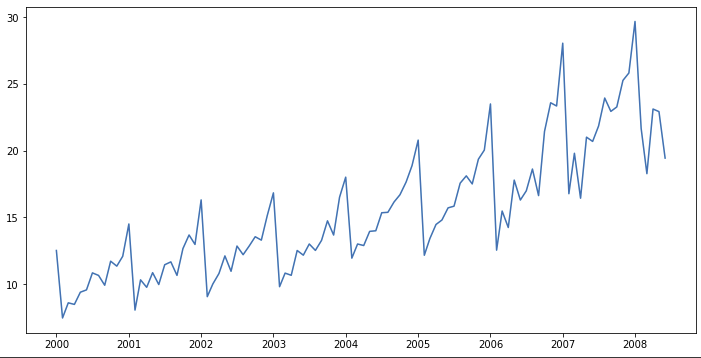
계절성은 특정 행동의 빈도가 안정적으로, 반복해서 나타나는 것이다. 위의 그래프를 보면 1년 주기로 특정한 형태를 반복적으로 띄는데 이러한 데이터를 계절성 데이터(Seasonal Data)라고 한다. 추가로 조금씩 증가하는 양상을 보이는데 이를 추세(Trend)라고한다.
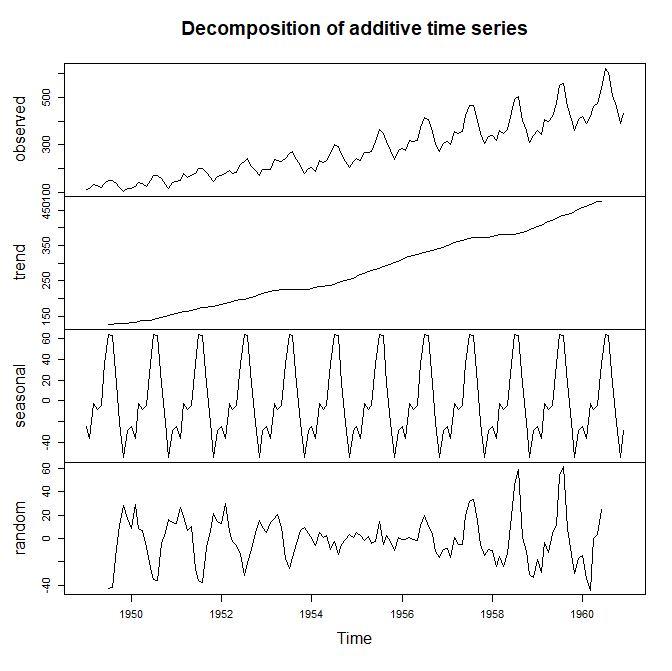
R이나 파이썬 모듈에는 이러한 그래프의 계절성, 추세, 그리고 noise를 Decompose 해서 보여주는 모듈이 존재한다.
시간대
파이썬 datetime module에서 시간대는 항상 UTC 기준으로 주어지지 않음.
내 컴퓨터 기준으로는 UTC로 나오는 것 같다.
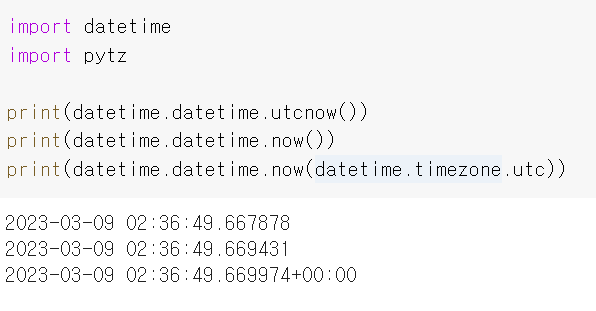
현지화된 시간 계산을 위해서는 아래 코드처럼 pytz 객체를 먼저 생성 한 뒤, Localize 함수를 사용한다.
*datetime module에 timezone 정보를 넣는 방법은 다른 결과를 가져올 수도 있다.
western = pytz.timezone('US/Pacific')
loc_dt = western.localize(datetime.datetime(2018, 5, 15, 12, 34, 0))'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-3 홀트-윈터스와 분해법 (0) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-2 지수평활법 (2) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-1 이동평균법 (0) | 2023.03.13 |
| 시계열 데이터 EDA (실전 시계열 분석 3장) (0) | 2023.03.09 |



