*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
지수평활법(Exponential Smoothing)
- 평활치를 구하는데 전체 데이터를 사용하며 시간에 따라 다른 가중치를 줌
- 과거로 갈수록 지수적으로 감소하는 가중치 사용
단순 지수평활(Simple Exponential Smoothing)
- 시계열 데이터가 수평적 패턴인 경우 사용
- $\alpha$ = $[0,1]$, $\alpha$가 클 수록 현재 시점에 더 가중치를 둔다
- 알파가 작을 수록 변동이 심한 현재 시점보다는 과거의 시점에 더 가중치를 둠으로서 Smoothing 효과가 더 커진다.
- 최근 데이터와 이전 지수평활의 가중평균

아래 그림을 통해 볼 수 있듯이, $\alpha$가 적을 때가 훨씬 평활 효과가 크다.

이중 지수평활(Double Exponential Smoothing)
- 시계열 데이터가 추세 패턴을 따르는 경우 사용
- 이중 이동평균과 마찬가지로 파라미터가 두 개이므로 두번의 Expectation이 필요.
- $E[S_t]$를 그냥 구하면 bias가 생긴다. -> 이를 보정하기 위해 이중 지수평활을 이용

자세한 증명 과정은 아래와 같다.
*증명과정은 아래 블로그를 참조하였습니다.
https://datalabbit.tistory.com/76
[시계열분석] 이중지수평활법(Double Exponential Smoothing Method)
Review 참고 포스팅 : 2020/11/16 - [Statistics/Time Series Analysis] - [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method) [시계열분석] 단순지수평활법(Simple Exponential Smoothing Method) 안녕하십니까, 간토
datalabbit.tistory.com

예측 역시 이중 이동평균법과 비슷하게, 예측하고자 하는 값
$$ c+b(T+1) $$
에 대해, $c$와 $b$의 추정치를 구할 수 있으므로 아래와 같은 방법으로 예측값을 도출할 수 있으며, $k$ 단계 역시 기울기의 계수에 더해주는 방식으로 구해질 수 있다.

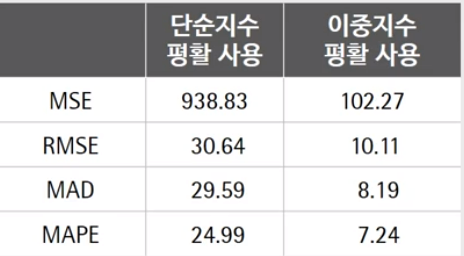
아래 결과를 살펴보면 단순 지수 평활법보다는 이중 지수 평활법이 훨씬 예측 성능이 좋은 것을 확인할 수 있다.
홀트 모형(Holt's Model)
- 시계열 데이터가 추세 패턴을 따르는 경우 사용
이중 지수 평활법과 비슷하나, 수평수준과 추세를 각각 다른 변수로 설정하고, $\alpha$, $\beta$의 하이퍼 파라미터를 이용해 각 변수를 업데이트 한다.

Quiz 3 풀이
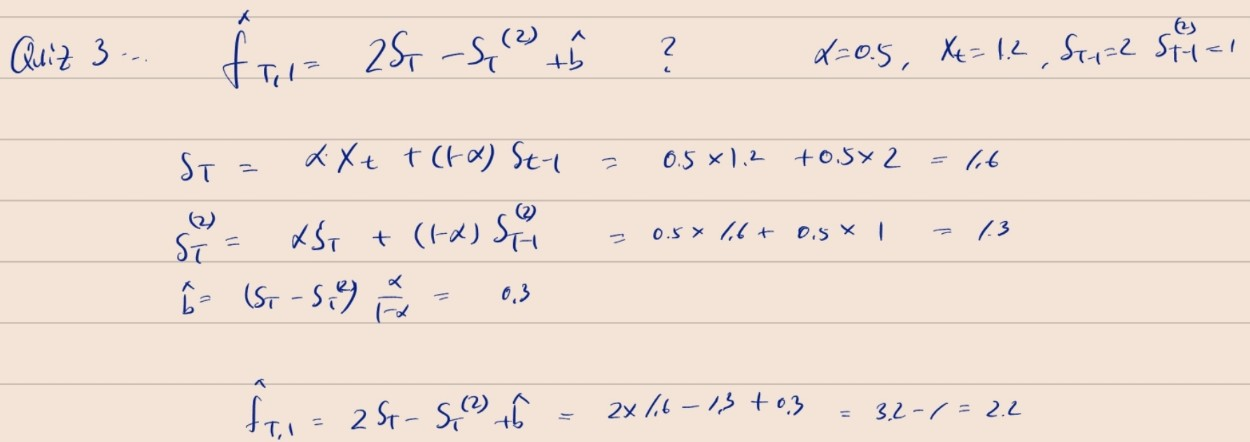
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-3 홀트-윈터스와 분해법 (0) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-1 이동평균법 (0) | 2023.03.13 |
| 시계열 데이터 EDA (실전 시계열 분석 3장) (0) | 2023.03.09 |
| 시계열 데이터 전처리 방법(실전 시계열 분석 2장) (0) | 2023.03.09 |



