*이 글은 실전 시계열 분석 책을 기반으로 작성되었습니다.

시계열 데이터의 EDA
3장에서는 탐색적 자료 분석 즉 EDA 과정에 대해 다룬다.
데이터간 어떤 상관관계?
데이터의 평균과 분산은?
이를 확인하기 위해, 도표, 요약 통계, 히스토그램, 산점도 등을 '시간'과 함께 고려해야 한다.
히스토그램
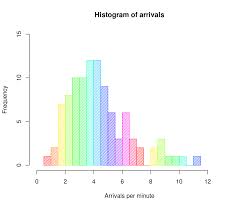
히스토그램 Draw 시에 X축을 시간, Y축을 변수 정보로 그릴 수도 있으나, Y축에 이전 변수와의 차이를 매핑하는 방법으로 새로운 아이디어를 얻을 수 있다. (R 코드에서 diff() 함수로 쉽게 구현 가능하다.)
산점도
시간의 흐름에 맞춰서 산점도를 mapping 하면 상관관계를 엿볼 수 있다.
두 주가 사이의 상관관계를 파악하기 위해 산점도를 그냥, 차분해서 매핑 했을 때, 상관관계가 높아 보일 수 있으나, 예측의 측면에서 바라보려면 예측하고자 하는 주가에 lag를 주어 한 시점 뒤로 미루고 산점도를 찍어봐야함. -> 상관관계가 실제로는 높지 않을 수 있다.
정상성 (Stationary)
정상 시계열 : 시간이 경과하더라도 안정적인 통계적 속성을 가진다. (평균과 분산)
정상성임을 증명하는 것보다 아님을 보여주는 것이 더 쉬움
아래 데이터 셋의 경우 시간의 경과에 따라 평균과 분산이 증가함을 확인할 수 있다. 추가로 계절성 또한 가지는데 이 또한 정상성에 반대되는 것.
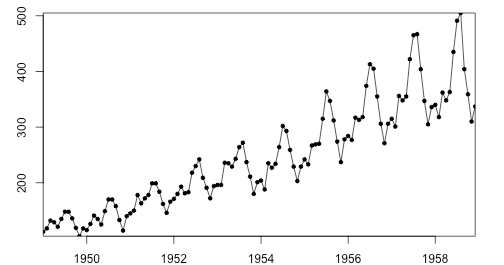
정상성의 정의 : 모든 시차 k에 대해서 yt, yt+1 ... yt+k의 분포가 t에 의존적이지 않으면 정상이다.
즉 시간에 따라 평균 분산이 일정한 성질
통계적인 검정 방법으로는 단위근(unit root)의 존재 유무로 판별할 수 있다.
yt = pi * yt-1 + ei
위 식에서 만약 pi값이 1이면 단위근이 있다는 의미이며 단위근이 있다는 의미는 비정상이라고 볼 수 있다.
하지만 단위근이 없다 = 정상성을 띈다는 아님.
디키-풀러 검정(augmented Dickey-Fuller, ADF):
시계열의 정상성 문제를 가장 보편적으로 평가하는 평가지표. 차분까지 고려한다. (많은 시차를 고려)
귀무가설 (h0) : 시계열에 단위근이 존재한다. -> t-test 결과 이용 -> 특정 유의도에 따라 기각하는 방식으로 단위근의 존재가 기각될 수 있음.
다만 이러한 검정은 단위근과 준단위근 구분 능력이 낮고, False positive 구분 능력이 낮음. (아닌데 맞다고 함)
ADF 제외하고도 KPSS 등 많은 검정 방식이 있으나 모든 종류의 문제를 해결하지 못하고, Task에 따라 다르게 특화되어 있다. (EX: 평균, 분산 정상인지 특화, 전체 분포보다는 일반적 부분을 검정 등) -> 일관적 한계점을 이해하고, 사용하자.
정상성이 중요한 이유 : 대부분의 전통적인 모델, 통계모델 등이 데이터의 정상성을 가정하기 때문. 비정상 평균과 분산을 사용하면 시간이 지날 수록 모델의 편향과 오차가 달라지고 모델의 가치가 떨어진다.
정상화 하는 방법론 : 분산이 변화하는 경우 log 나 제곱근을 씌워준다, Trend, Seasonal 의 경우 차분을 구하고 제거하는 것이 일반적이다.
로그나 제곱근 변환을 사용하려면 데이터가 항상 양(positive) 라는 가정이 필요하며 이상치 존재여부를 꼭 살펴야 한다.
정상성 외에도 정규성을 고려해야함 . -> 박스-칵스 변환Box-Cox transformation
자체상관 (Self Correlation), 자기 상관 (Auto Correlation)
시계열 그 자체로 연관성이 있다는 의미. 내제된 역동성
자기상관 : 어떤 신호와 자신을 자연 함수로 시간상 지연 이동한 신호 간의 상관관계이다.
ACF: Autocorrelation Function 자기상관함수.
코드로는 다음과 같다.(R)
cor(y, shift(y,1), use = "pairwise.complete.obs")현재 시점, 이전 시점의 correlation 을 구하는 것이라고 생각하면 된다.
ACF의 특징 :
- ACF의 주기함수는 원래 과정과 동일한 주기성을 띈다 (Sin 함수)
- 주기함수들의 합의 자기 상관은 각 개별 함수에 대한 자기상관의 합이다.
- 시차가 0 일때 모든 시계열의 자기 상관계수는 1이다.
- white noise는 시차가 0일때를 제외하고는 모두 자기 상관 계수가 거의 0에 가깝다.
- ACF는 양 음의 시차에 대해 대칭을 이룬다. 따라서 양의 시차만 고려할 수도 있다.
- 0이 아닌 유효한 ACF 추정을 결정하는 규칙은 +=1.96 x sqrt(n)의 임계영역을 사용하는 것(X축의 domain). 충분히 큰 샘플 크기에서의 유한 분산에서만 유효하다.
PACF (partial autocorrelation function) 편자기상관함수
ACF의 경우에는 yt 와 yt+k 사이의 correlation 을 구할 때 그 사이의 yt+1 ~ yt+k-1 을 모두 고려하는 반면, 편자기상관의 경우 그 사이의 영향을 배제한다는 특징이 있다.
ACF와 PACF의 내용은 다음 블로그를 참조하는 것이 더 좋을 듯 하다.
ARIMA란? :: ARIMA 분석기법, AR, MA, ACF, PACF, 정상성이란?
앞 서, 시계열 데이터와 시계열 분석에 대한 간단한 설명과 시계열 분해법에 대해 설명했다. 2021.05.24 - [통계 지식/시계열자료 분석] - 시계열 분해란?(Time Series Decomposition) :: 시계열 분석이란? 시
leedakyeong.tistory.com
허위상관 (Spurious Correlation)
상관관계가 허위일 수 있음.
계절성: 핫도그 소비와 익사의 상관관계 (둘 다 여름에 주로 발생)
누적합계: 무조건 증가할 수 밖에 없는 누적 합게를 이용해서 증가하는 것 처럼 속임수로 사용
공적분(cointegration) : 두 시계열 사이의 진짜 관계
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-3 홀트-윈터스와 분해법 (0) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-2 지수평활법 (2) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-1 이동평균법 (0) | 2023.03.13 |
| 시계열 데이터 전처리 방법(실전 시계열 분석 2장) (0) | 2023.03.09 |



