*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
추세와 계절성이 있는 시계열에 적용
윈터스 (Winters) 모형
- 홀트 모형에 계절성 (seasonality)을 추가반영하여 확장시킴
- 가법 (additive) 모형과 승법 (multiplicative) 모형이 있음 - 강의에서는 승법만 설명
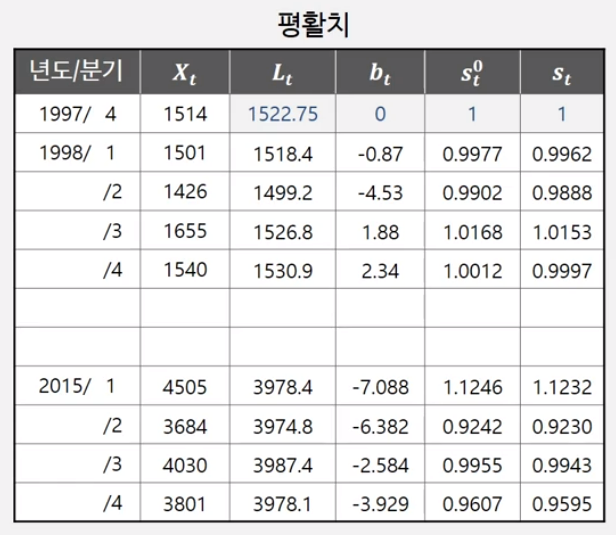
-$s_t$ : 기존 홀트 방법에서는 추세 $bt$ 변수 까지만 존재하였음. Winters에는 계절성 지수 $s_t$가 추가됨. $t=1, \ldots ,m$
-$m$ : 계절성 공식의 $m$은 계절의 주기를 나타내는 것으로, 분기별 데이터의 경우 $m=4$, 월별이면 12, 주별이면 7

- $\alpha, \beta, \gamma$의 최적값을 찾는 소프트웨어도 존재한다.
- 처음에 initializing이 필요하며, 계절성 지수는 평균이 1이 되어야 한다.
분해법 (Decomposition)
- 추세와 계절성을 분해한 후 예측시 다시 결합
- 가법모형과 승법모형이 있음
가법적 모형에서는 추세, 계절성, 오차의 요인이 더해지는 형태로 구성, 계절성의 합은 0
가법적 모형에서는 추세, 계절성, 오차의 요인이 곱해지는 형태로 구성, 계절성의 합은 $m$ (평균은 1)

분해법에 의한 예측 절차
- 중심이동평균(Centered moving average)로 평활치 산출 ---> 전 후 데이터를 이용해서 평균을 낸다.
- 추세 제거(detrended) 시계열 산출 ---- 계절성을 계산하기 위한 단계
- 계절성 지수 산출
- 계절성 제거(deseasonalized) 시계열 산출
- 회귀모형으로 추세 추정 --- 실제 추세 제거
- 추세 및 계절성 지수를 결합하여 예측치 산출
1. 중심이동평균(Centered moving average)로 평활치 산출
$m$ 즉 주기가 홀수인 경우에는 데이터의 중심이 한번에 정의되므로 그냥 평균을 낸다.
주기가 짝수인 경우에는 해당되는 시점 반경의 앞과 뒤 데이터를 0.5 씩 곱해서 더해준 뒤 평균을 낸다.
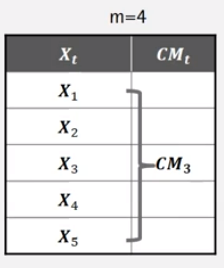
예를 들어, 오른쪽 아래 처럼 $m=4$일 때 $X_3$에 대한 $CM_3$를 구하기 위해서는, $X_1~X_5$의 평균을 구한다.
만약 $m=5$일 때 $X_4$에 대한 $CM_4$를 구하려면 아래 식으로 구한다.
$$ (X_1/2 + X_2 + X_3 + X_4 + X_5 + X_6 + X_7/2)/5 $$

2. 추세 제거(detrended) 시계열 산출 ---- 계절성을 계산하기 위한 단계
이렇게 얻어낸 $CM_t$를 $X_t$에 나누어 줌으로서 추세가 제거된 시계열을 얻는다.

3. 계절성 지수 산출
얻어진 추세제거 시계열 값의 평균으로 계절성 지수 $s_i, i=1 \ldots m$을 산출한다. (1분기 데이터의 평균, 2분기 데이터의 평균 $\ldots $)
이때 계절성 지수 평균이 1이 되어야 한다.
4. 계절성 제거(deseasonalized) 시계열 산출
다시 $X_t$를 $s_t$로 나누어 계절성이 제거된 시계열을 얻어낸다.
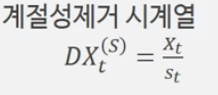
5. 회귀모형으로 추세 추정 --- 실제 추세 제거
회귀분석을 이용해 추세를 찾는다. (1차식, 2차식...)
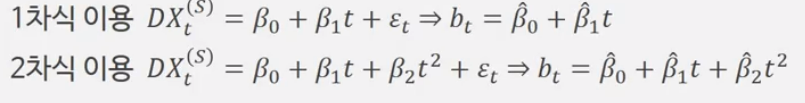
6. 추세 및 계절성 지수를 결합하여 예측치 산출
회귀분석으로 얻어낸 식과 계절성의 곱으로 예측치를 산출한다.
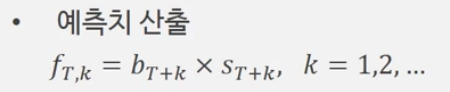
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-2 편자기상관함수, AR/MA 표현방식, 후향연산자 (0) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-2 지수평활법 (2) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-1 이동평균법 (0) | 2023.03.13 |
| 시계열 데이터 EDA (실전 시계열 분석 3장) (0) | 2023.03.09 |



