*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
ARCH 모형
이번 장에서는 ARCH(Autoregressive Conditional heteroskedasticity) 모형에 대해서 다룬다.
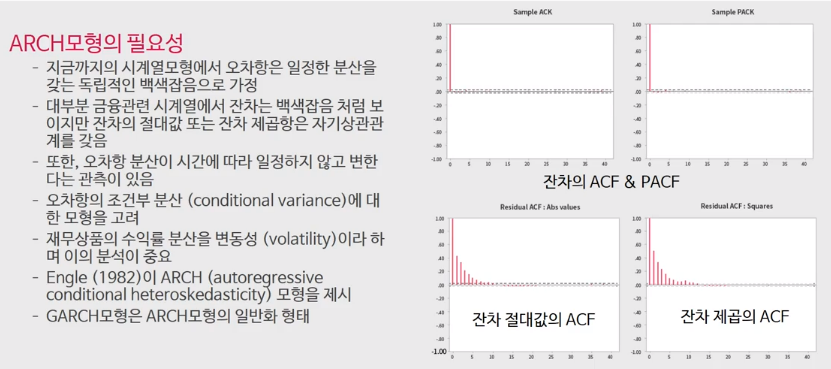
week 1~4까지는 오차항 $a_t$이 white noise라는 가정을 통해 시계열 모델을 구축했으나, 현실에서는 잔차 역시 완전히 설명되지 않은 경우가 많다. 금융데이터가 대표적으로 잔차의 ACF&PACF는 0의 형태를 띄는 것으로 보이나, 잔차에 절대값이나 제곱을 씌워서 다시 그려보면 위 그림처럼 자기상관관계가 존재하는 경우가 많다고 한다. 또한 연구결과에 따르면 오차항(Residual)의 분산이 시간에 따라 일정하지 않고 변한다는 관측이 존재한다.
이에, 오차항의 조건부 분산 또한 고려해야한다는 논의가 제기되었고, 특히 금융상품에 대해서는 이러한 '변동성'을 이용해 수익률을 분석하기 때문에 이를 위한 ARCH(Autoregressive Conditional *heteroskedasticity)모형이 등장하게 된다.
*여기서 heteroskedasticity는 분산이 같지 않다는 뜻 (이異분산성)
ARCH 모형의 표현

ARCH 모형을 어떻게 표현하는지 살펴보면, 이전에 SARIMA에서 다뤘던 접근법과 비슷하게 오차항이 특정한 관계를 갖는다는 가정이 추가된 형태이다. 다른점은 오차 제곱항에 대한 관계를 표현했다는 점과 AR 모형을 따른다는 가정으로 바뀌었다.
$$u_t^2 = \alpha_0 + \alpha_1u_{t-1}^2 + \dots + \alpha_qu_{t-q}^2 + w_t (w_t : white noise)$$
여기에 오차항의 조건부 분산을 구하면,
$Var[u_t|u_{t-1},...] = E[u_t^2|u_{t-1},...]-E[u_t|u_{t-1},...]^2$ 인데, 오차항의 평균 즉 $E[u_t|u_{t-1},...] = 0$이므로, $Var[u_t|u_{t-1},...] = E[u_t^2|u_{t-1},...]$이 되고, $E[w_t] = 0$이고 $u_{t-1}^2...u_{t-q}^2$은 이미 확인한 오차항 즉 상수이므로 최종적으로 다음과 같은 식의 형태가 된다.
$$\sigma_t^2 = Var[u_t|u_{t-1},...] = E[u_t^2|u_{t-1},...] = \alpha_0 + \alpha_1u_{t-1}^2 + \dots + \alpha_qu_{t-1}^2$$
이에 아래와 같은 형태의 모형을 ARCH(q) 모형이라고 한다.
$$\sigma_t^2 = \alpha_0 + \alpha_1u_{t-1}^2 + \dots + \alpha_qu_{t-1}^2$$
ARCH 모형의 정상성 조건
ARCH 모형에도 정상성 조건이 필요하다.
정의상 오차항의 분산 (조건 없는 분산)은 시간에 따라 일정한 상수 $\sigma_u^2$이 되나, 오차항의 조건부 분산인 $\sigma_t^2$는 whilte noise가 제거된 *MA 모형을 따르며 시간에 따라 변화한다.
*아까까지는 AR모형을 따른다고 했던 것 같은데 갑자기 왜 MA라고 하냐면, ARCH의 가정은 제곱오차항 즉 $u_t^2$이 AR모형을 따른다고 가정을 하고 만든 것이어서 제곱오차항은 AR을 따르는게 맞지만, 이를 통해 유도해낸 $\sigma_t^2$는 본인 자기 자신에 대한 식이 아니라 제곱오차항에 대한 식이 되므로 MA모형의 형태를 띈다고 봐야한다.

조건부 분산$\sigma_t^2$에 대해 기대치를 취하면 조건없는 분산과 같게 되고, 이를 이용해 식을 유도하면 ARCH 모형이 정상적인 경우 아래와 같은 식이 성립해야 한다고 한다. (자세한 유도과정은 다루지 않았다.)
$$\sigma_u^2 = \frac{\alpha_0}{1-\alpha_1-\dots-\alpha_q}$$
여기서 분산의 경우 0보다 커야하므로 정상성 조건은 $\alpha_1 + \dots + \alpha_q < 1$이 된다.
평균 방정식과 분산 방정식

ARCH 모형은 원래 시계열이 존재하고, 여기에 추가로 오차항을 다루는 모형이 존재하는 형태. 이를 분산 방정식이라고 한다. 강의에서는 아래와 같이 개념을 정리한다.
- 시계열 자체의 모형 : 평균 방정식
- 오차항의 모형 : 분산 방정식
따라서 ARCH가 포함된 시계열 모형은 [시계열모형이름] - ARCH(q) 모형의 형태로 쓰며, 오차항을 포함하는 평균방정식과, 오차항에 대한 분산방정식을 동시에 정의해야한다. 위의 그림에서 볼 수 있듯이 시계열이 AR, MA의 일종이 아니더라도 사용할 수 있다.
ARCH-M 모형

ARCH-M도 자주사용한다고 하는데, 평균방정식 안에 조건부 분산을 포함시킨 모형을 의미한다. (말 그대로 ARCH in mean equation) 위에서의 다른 예시들과는 다르게 평균방정식 안에 $u_t$ 뿐만 아니라 조건부분산$\sigma_t^2$에 대한 함수 또한 정의되어 사용된 것을 확인할 수 있다.
즉 조건부 분산 또한 Y를 설명하는데 관여가 된다고 판단되는 경우 사용되는 모형이다. 꼭 $\sigma_t^2$의 형태가 아니더라도 루트를 씌운 꼴이나 다른 형태여도 상관없이 변수 자체가 들어가는 경우 이를 ARCH-M 모형이라고 한다.
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-3 GARCH 모형의 추정과 관련 검정 (0) | 2023.03.28 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-2 GARCH: ARCH의 일반화 형태 (0) | 2023.03.28 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week4-2 계절성을 반영한 ARIMA 모형 이해 (0) | 2023.03.22 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week4-1 비정상적 시계열 모형화를 위한 ARIMA 모형 (0) | 2023.03.22 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week3-3 최소평균오차 기반의 ARMA 모형 예측치 유도 (0) | 2023.03.15 |



