*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
이번에는 GARCH, ARCH모형의 추정에 대해 살펴보자.
ARCH 모형의 추정
먼저 조건부 오차 $u_t|u_t-1,...$이 정규분포를 따를 때, 이를 이용해서 아래와 같은 로그우도함수를 유도할 수 있고, 평균방정식이 회귀모형인 경우 $y_t = x_t\beta + u_t$인데, 이를 다시 $u_t$에 대해 정리하면 아래와 같은 $u_t = y_t - x_t\beta$를 얻을 수 있다.

문제는 시차 q를 정해야하는데, ARMA 모형처럼 ACF 등 어떤 형태를 보고 판단하는 것이 아니라, 직접 넣어보고 결정하는 방식을 선택한다고 한다.
아래 예시를 보면 AR(1)-ARCH(q)모형의 파라미터를 추정하는데 파라미터 추정과 적절한 q값을 찾는 것을 동시에 진행하게 된다.
여기서 추정해야할 파라미터는 $c, \phi, \alpha_0 ~ \alpha_q$이다. 최대우도추정법을 이용해 각 모델 q=1,2,3,4에 적합한 파라미터들을 추정한 뒤, 정보기준 SC, HQ, AIC가 작은 것을 기준으로 적절한 q를 선택한다.

이렇게 모델이 결정되고 파라미터가 추정되면, 이렇게 얻어낸 ARCH(q)모형이 과연 효용이 있는지를 검정하는 LM 검정을 수행한다.
LM (Lagrange multiplier) 검정

귀무가설은 $\alpha_1 ~ \alpha_q$가 모두 0이다. 이는 다시말해 ARCH 모형이 의미가 없다는 것을 뜻한다.
검정 방식은 모형(여기서 모형은 ARCH를 적용하기 이전, AR(1)-ARCH(1)이면 AR(1)을 의미)을 추정한 뒤, 잔차 $u_t$를 구하고, 이를 이용한 AR모형의 $R^2$를 산출해서 검정통계량 $LM = n \times R^2$를 구한다. 이렇게 구한 검정 통계량 LM이 카이제곱분포의 기각역을 벗어나는 경우 가설을 기각한다.
귀무가설이 "ARCH 모형이 의미가 없다." 이므로 기각은 즉 ARCH 모형이 효과가 있다는 의미이다.
예시를 통해 살펴보면

통계량 LM이 121.667 그리고 p-value (Prob. Chi-Square(4))가 0으로, 기각 즉 ARCH 모형이 추가되어야 함을 의미한다.
GARCH 모형의 추정

GARCH 모형의 추정 역시 동일하고, 조건부 분산항 부분만 beta항이 추가된다.
GARCH(1,1)를 추정하는 예시를 통해 살펴보면, 아래 오른쪽 그림의 Variable column 에서 RESID(-1)^2 부분은 ARCH term $\alpha_1$, GARCH(-1)는 GARCH term $\beta_1$을 의미한다. 우측의 prob 즉 p_value를 살펴보면 $\alpha_1$의 경우 기각에 실패 즉 유의하지 않다는 것을 보여준다.

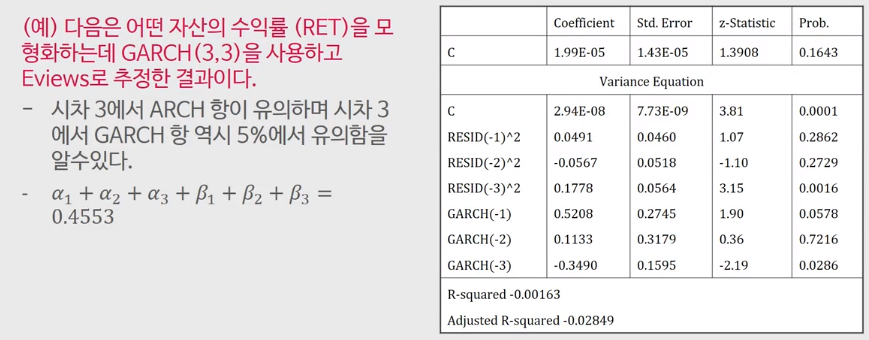
이번엔 GARCH(3,3)을 추정하는 예시를 살펴보자 추정된 $\alpha, \beta$를 모두 더해보면 정상성을 만족함을 확인할 수 있고, 둘 다 세번째 시차에서 유의함을 확인할 수 있다.
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week6-2 충격-반응함수의 이론과 응용, 예측오차 분산분해 (0) | 2023.03.29 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week6-1 VAR 모형의 식별 및 추정 이론 (0) | 2023.03.29 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-2 GARCH: ARCH의 일반화 형태 (0) | 2023.03.28 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week5-1 오차의 조건부 분산 개념 및 ARCH 모형 (0) | 2023.03.28 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week4-2 계절성을 반영한 ARIMA 모형 이해 (0) | 2023.03.22 |



