*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.
편자기상관함수 (Partial Autocorrelation function, PACF)
- 정상적 시계열의 형태를 식별하는데 ACF 외에 PACF의 정보를 활용함.
- 내가 고려하고자 하는 시점 $t, t-k$ 사이의 중간 시점들 $(t-1, t-2, ... t-k+1)$에 대한 정보가 주어진 상태의 Correlation.
- 따라서 중간값이 없는 $P(1)$의 경우 조건부 확률이 제외되므로, ACF와 동일한 값을 가지게 된다.
- 아래 회귀식을 살펴보면 $Z_t$를 설명하기 위해 이전 정보들 $Z_{t-1} ~ Z_{t-k}$의 선형결합을 진행 했을 때, $t-k$의 계수와 동일하다고 볼 수 있다.
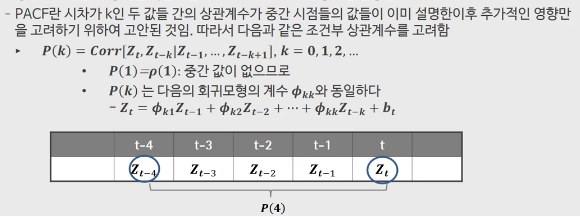
이렇게 얻어진 식의 양 변을 $Z_{t-1}, Z_{t-2} \ldots Z_{t-k}$와의 상관계수 form으로 변형하면 아래 $k$개의 식이 유도된다.
이를 연립방정식으로 풀어 PACF를 계산할 수 있다.

시계열의 표현 방식
크게 두 가지 방식을 사용한다.
- 자기회귀 (autoregressive; AR) 표현방식

- 이동평균 (moving average; MA) 표현방식

이전 포스트에서 다룬 예제 1과 예제 2에서 모두 확인해 본 것들이다.
이러한 두 표현방법을 더 간단하게 나타내는 방법으로 후향연산자가 있다.
후향연산자 (Backward Shift Operator, Backshift Operator)
말 그대로 $B$를 곱한다는 의미를 한 시점 이전으로 간다는 의미로 대체하는것.
$n$번 뒤의 시점을 나타낼 때는 $B^n$의 형태로 표기한다.

이렇게 후향연산자를 사용하면, 두 표현 방식에서 모두 $Z_t$에 관해 묶을 수 있다는 이점이 있다.
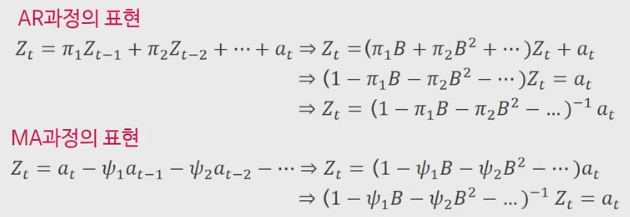
'데이터 과학 스터디 > 시계열 스터디' 카테고리의 다른 글
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-4 ARMA모형 (0) | 2023.03.15 |
|---|---|
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-3 AR모형 및 MA모형의 표현 및 성질 규명 (0) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수 (1) | 2023.03.15 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-3 홀트-윈터스와 분해법 (0) | 2023.03.14 |
| 시계열 분석 기법과 응용[Postec 전치혁 교수] Week1-2 지수평활법 (2) | 2023.03.14 |



