시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-3 AR모형 및 MA모형의 표현 및 성질 규명

*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.

 

ARMA

ARMA 모형

- AR 과 MA 표현 방식이 결합된 형태

- ARMA(1,1): 시차 1의 변수와 시차 1의 백색잡음 포함

- week2-3에서는 다루지 않는다.

 

AR 모형

- AR 표현방식이며 유한 시차로 구성

- AR(1): 시차 1 변수 포함, 가장 단순한 형태

AR(1) formula

AR(2) 모형부터 정상성 조건이 복잡해진다. (유도과정도 어렵다고 한다.)

 

AR(1) 모형의 ACF와 PACF를 살펴보자. 

*ACF를 구하는 증명은 이전 포스팅 Week 2-1에서 다룬바 있다.

https://uky-note.tistory.com/29

시계열 분석 기법과 응용[Postec 전치혁 교수] Week2-1 정상적 시계열과 자기상관함수

• AR(1)모형의 ACF, PACF

$-1< \phi _1 <1$ 이고 ACF는 $\phi _1$의 k승 형태가 되기 때문에, 시차가 커지면 커질 수록 지수적으로 감소한다.

PACF의 경우 $\phi _2$자체가 정의되지 않아 $k = 2$부터는 $0$이된다. 이를 절단패턴이라고 한다.

• AR(2)모형의 ACF, PACF

AR(2)의 경우 유도가 복잡해 강의에서는 이를 다루지 않았으나, 지수적으로 감소하는 패턴 자체는 동일했다.

PACF 역시 $\phi _3$부터 정의되지 않으므로, 3시차부터 절단패턴의 형태를 띈다.

• AR(p)모형의 ACF

Yule-Walker 방정식으로 ACF를 산출할 수 있고, 아래 그림 윗단에 있는  $\Phi _p(B)=0$ 으로 정상성을 판별할 수 있다고 한다.

 

MA 모형

- MA 표현방식이며 유한 시차로 구성

- MA(1): 시차 1 백색잡음 포함

MA(1) formula

MA 모형의 경우 AR형태 표현을 위해, inverse를 취해야 해서 $\theta$에 대한 invertibility 조건이 필요하다.

(Example)

• MA 모형의 ACF, PACF

MA모형은 ACF가 시차 $q$이후에 절단 패턴을, PACF가 지수적인 감소패턴을 띈다는 공통점이 있으며, 분산의 경우 구하기 쉬우나 $\theta$에 대한 가역성 조건이 꽤나 까다롭다.

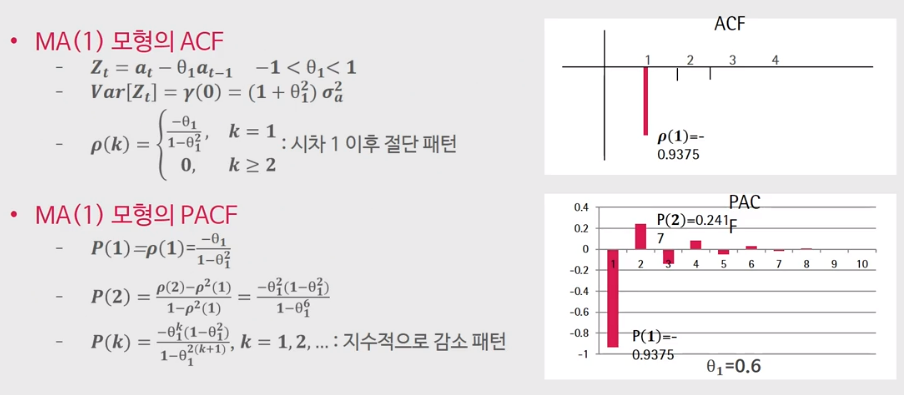
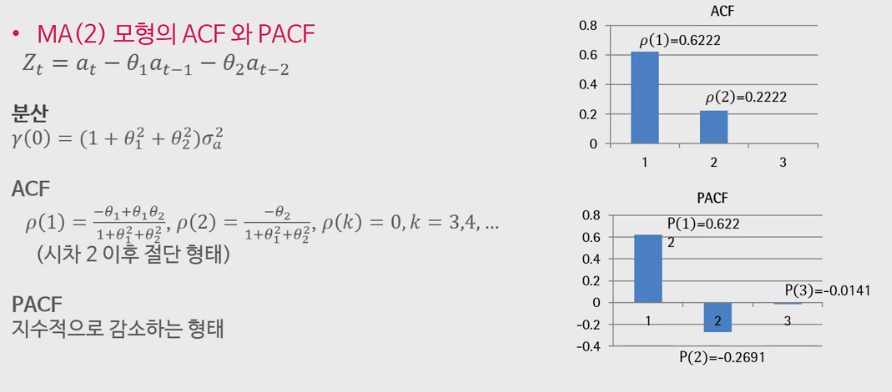
MA모형에서는 위 그림의 $\theta(q) = 0$의 근의 크기가 $1$보다 크면 invertible하다.

 

두 모형을 정리해보면 아래와 같다.

	AR(q) 모형	MA(q) 모형
분산	구하기 어려움	구하기 쉬움
정상성	정상성 조건 확인 필요	항상 정상성을 띈다
가역성	조건 필요 없음	AR 모형으로 변형하기 위한 가역성(Invertibility) 조건 확인 필요
ACF 형태	지수적으로 감소	q 시점 이후 절단패턴
PACF 형태	q 시점 이후 절단패턴	지수적으로 감소