시계열 분석 기법과 응용[Postec 전치혁 교수] Week6-3 공적분의 개념과 가성회귀, 오차수정모형의 이론 및 응용

*이 포스트는 포스택 전치혁 교수님의 K-mooc 강의, 시계열 분석 기법과 응용을 기반으로 작성되었습니다.

 

지난번에는 왼쪽 즉 정상적 시계열 분석에 대해 알아보았다면, 이번에는 비정상적 시계열 분석에 대해 다룬다.

비정상적 시계열 분석

가장 먼저 당연히 정상적 시계열보다는 비정상적 데이터가 훨씬 많다.

• 경제/금융 시계열 각각은 비정상적이나, 소득과 소비처럼 장기적으로는 서로가 서로를 따라가는 관계가 있는 경우가 있고, 이를 공적분(Cointegration) 관계라고한다.
• 차분을 통해 정상적 시계열 변환보다는 이를 그대로 사용하는게 더 많은 정보를 얻을 수 있다.
• 비정상적 시계열인데 서로 관련이 없는 경우에도 함께 증가하는 경우 이를 상관관계가 있다고 해버리는 가짜 상관관계를 가성 회귀(spurious regression)이라고 한다. 따라서 이를 피하기 위해, 동일 차수의 누적 시계열에 대해서만 공적분 분석을 사용해야한다.

누적벡터시계열

따라서 먼저 누적 벡터시계열과 공적분의 정의부터 다시한번 살펴보자.

ARIMA 모형에서 차수 d 누적시계열의 개념을 다뤘었는데, 시계열이 벡터형식으로 변한것 외에는 모두 같은 내용이다. 비정상적 벡터시계열 $x_t$를 d차 차분했을 때, 처음으로 정상적이 되는 경우, $x_t$ 를 차수 d의 누적벡터시계열이라고 한다.

공적분

I(d)의 누적 벡터시계열에 벡터 $\alpha$를 dot-product 시켰을 때, 차수 d 미만의 누적시계열이 될 때 이러한 공적분 벡터 $\alpha$를 갖는 공적분 관계에 있다고 한다.

예를 들면 2번 차분을 해야 정상성을 만족하는 2차차분시계열이 있는데 공적분 벡터 $\alpha$랑 선형결합을 했더니, 한번만 차분을 해도 정상성을 만족하는 시계열이 된다고 하면, 누적 벡터시계열이 공적분 벡터 $\alpha$를 갖는 공적분 관계에 있다고 정의한다.

벡터 시계열 $x_t$안에 m개의 시계열($Z_{1t}, Z_{2t} \dots$)이 있을 때, 이런 조건을 만족하는 $\alpha$의 개수가 최대 m-1개 존재할 수 있다. 이 때 m-1을 공적분 랭크 (cointegration rank)라고 한다.

 

오차수정모형 (Error correction model; ECM)

그럼 공적분이 있다고 보였으면 이를 어떻게 이용하는가? 

공적분 관계가 있으면 오차수정모형(ECM)으로 표현이 가능하다.

ECM 유도 예시를 살펴보면, 시계열 $Y_t$와 $X_t$가 공적분 벡터 $\beta$를 갖는 관계에 있다고 하면, t-1 시점에서

$Y_{t-1} = \beta X_{t-1} + e_{t-1}$인데(이미 관측한 것이기 때문에 실제 오차인 e가 된다) 이것을 t시점에 더하고 빼주면, 아래와 같이 되고,

$$Y_t - (Y_{t-1} - Y_{t-1}) = \beta X_t + \beta(X_{t-1}-X_{t-1}) + \epsilon_t + e_{t-1} - e_{t-1}$$

$Y_t - Y_{t-1} = \Delta Y_t$, $X_t - X_{t-1} = \Delta X_t$의 차분의 형태로 위의 식을 정리하면 최종적으로 아래 형태가 된다.

$$\Delta Y_t  = -e_{t-1} + \beta \Delta X_t + \epsilon_t$$

이 식이 ECM의 가장 기본적 형태이다.

 

이를 일반적인 형태로 나타내면 minus(-) 대신 $\lambda$를 사용해서 아래와 같이 표기한다.

이러한 $\lambda$를 오차수정항이라고 부르는데, 예측오차를 보고 이에 따라 크거나 작으면 반대방향으로 Y값을 늘이거나 줄여서 X와 Y의 관계를 장기적으로 유지시킨다.

$\Delta X$가 변하면 $\Delta Y$가 변하는 것은 단기 효과로 볼 수 있다.

단순형태 ECM은 이전 시차 $t-1$만 고려했는데, 이러한 시차 역시 변수로 포함할 수 있고, Y에 대해서 뿐만아니라 X에대해서도 동일하게 적용시킬 수 있다. X에 관한 것과 Y에 관한 것을 동시에 쓰면 위 그림 가장 아래 벡터표현으로 나타낼 수있고 이를 벡터 ECM이라고 한다.

 

벡터 ECM (VECM)

따라서 벡터 시계열이 공적분 관계가 있으면 VECM으로 확장시킬 수 있고, 이렇게 VECM의 행렬 $\Pi$ 의 랭크에서 0~m사이인 경우에 행렬을 A와 B 두 개로 나눌 수 있고, 행렬 B에 대해 해석할 수 있어 이 경우를 집중해서 본다고 한다.

 

이제 실제로 공적분이 존재하는지 먼저 확인하는 검정을 살펴보고 VECM 모형을 추정하는 과정에 대해 알아보자.

 

공적분 검정

공적분 관계가 있는지 검정하는 방법으로 강의에서는 아래 두 가지 경우를 제시하며, Johansen 검정 안에도 두 가지 경우로 나뉘는데, E-views 소프트웨어에서 트레이스와 최대 고유치, 두 가지 검정결과를 모두 제공한다고 한다.

 

이제 예시를 통해 살펴보자

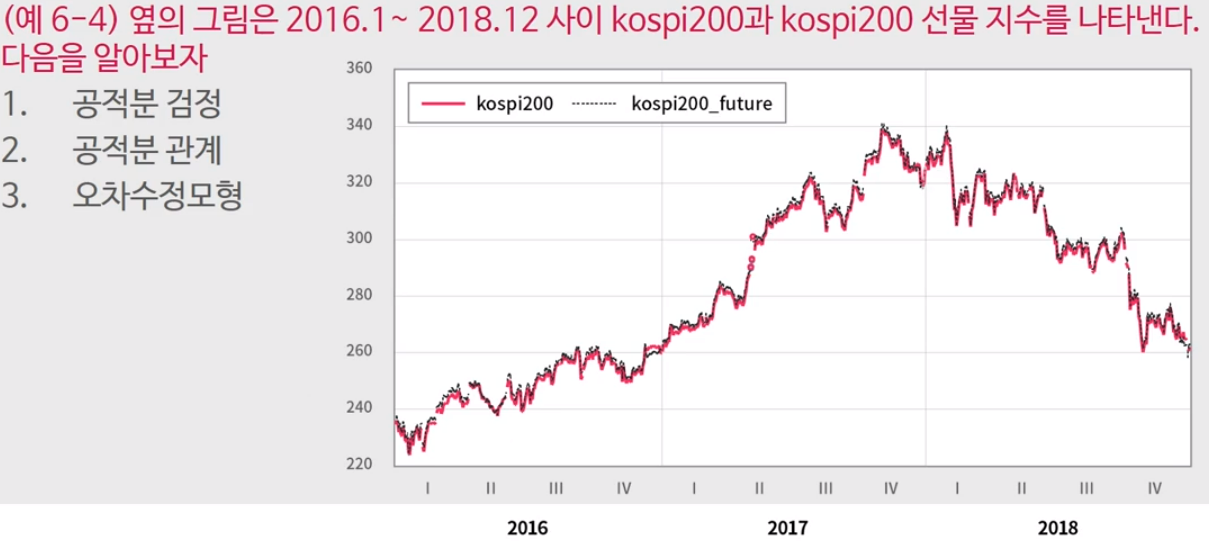
kospi 200과 kospi 200 선물 데이터인데, 두 시계열이 거의 겹쳐있어 눈으로 봐도 어느정도는 공적분 관계가 있을것으로 보인다.

공적분 검정 결과를 살펴보자. 그림 우측의 굵은 가로선 부분이 Trace 검정 결과 이고, 조금 아래로 내려가면 Unrestricted Cointegration Rank Test (Maximum Eigenvalue) 부분이 최대 고유치 검정의 결과이다.

H0:는 no Cointegration 즉 공적분이 없다 인데, 각 검정결과의 p-value를 보면 두 결과 모두 0으로 공적분이 한 개 이상 존재한다는 것을 확인할 수 있다. 그런데 시계열이 2개이므로 공적분은 최대 1개 존재하니 하나라고 볼 수 있다. (시계열이 m개면 최대 m-1개 존재가능)

 

공적분 관계가 있으면 항상 ECM모형으로 표현이 된다고 했다. 

아래는 E-views 프로그램을 통해 오차수정모형을 추정한 것이다.

위 그림의 공적분 관계식 부분을 보면 계수가 0.9987로 거의 1에 가까운 값을 가짐을 확인할 수 있다.

그리고 그 아래를 보면 2개의 오차 수정 모형이 얻어지는데, $e_{t-1}$앞의 계수를 살펴보면 코스피 200 선물은 오차가 생겨도 0.0622로 빠르게 조정하지 않지만, 코스피 200은 오차항 계수의 절댓값이 0.1183으로 선물지수와 차이가 발생시 빠르게 따라감을 확인할 수 있다.